선형회귀 분석에서 로그 변환을 취하는 이유

 

"Linear models love normally distributed data"
 
 

https://www.kaggle.com/code/serigne/stacked-regressions-top-4-on-leaderboard

 

캐글 커널에서 마주한 "Linear models love normally distributed data." 라는 문장의 맥락을 파헤쳐 보고자한다.

선형 모델들과 정규적인 분포의 데이터우 무슨 관계가 있길래 'love'라는 과감한 비유까지 든걸까?
 

 

우선 데이터의 분포라는 것은 통계 모델, 혹은 머신러닝 모델에서 독립변수와 종속변수, 설명변수와 반응변수 혹은 feature X와 target y도 불리는 예측 대상인  ①$y$값의 분포가 있고,

각 데이터 포인트의 특성(feature)의 집합인, ②$X$에 대한 분포가 있다.
(통상 예측 대상인 $y$는 스칼라이기에 소문자를 취하고, 독립 변수는 feature set이라고 불리는 특성의 집합들로 통상 구성되기 때문에 대문자 $X$로 표현하곤 한다.) 

선형회귀 분석을 공부하다보면, ①, ② 두 경우 모두 만약 분포의 형태가 정규 분포가 아니라 오른쪽으로 긴 꼬리 분포(right-skewed) 혹은 왼쪽으로 긴 꼬리 분포(left-skewed)의 상황이라면 로그 변환(log transformation), 박스 콕스 변환(Box-Cox Transformation) 등으로 부터 정규성을 확보해야 한다고 알려져 있다.
 
그러나 이러한 변환의 수행은 서로 다른 이유에 있다.

 

출처: https://ghd45698.tistory.com/23

 

① Target $y$ distribution

 
기본적으로 머신러닝 모델은 어떠한 패턴을 반영하기 위한 구조적인 특징, 학습과정에서 가지는 가정이나 선입견인 'inductive bias'를 갖는다.
선형회귀는 이름 자체에서 내포하고 있듯, 관측된 데이터의 특성$X$와 타겟$y$의 관계가 선형적이라는 inductivd bias와 
선형성을 포함한 대표적인 4가지 성질(선형성, 독립성, 정규성, 등분산성)을 가정한다.

 

그러나 이 4가지 성질에는 종종 주어가 생략되어 나를 포함한 많은 이들을 쉽게 혼란을 야기하는 듯하다.

 

대표적인 4가지 성질에 대해 주어를 덧붙여 서술하자면 (모델의 선형성, 잔차의 등분산성, 데이터의 독립성, 잔차의 정규성) 쯤이 될 것 같다. 이 중에서, 선형 모델이 정규 분포를 띈 데이터와 잘 맞는 것은 4번째 특징인 '잔차의 정규성'과 관련된 특징이며, 이들 각 성질에 대해서 각각 '모델, 잔차, 데이터, 잔차'의 주어가 의미하는 바를 간접적으로 살펴보려고 한다. 
 

 
 

 

잔차의 정규성 가정

 

예를 들어 우리가 관찰하고자 하는 타겟값이
아래의 scatter plot에서 Training data와 Validation Data로 표현되어 있고
이를 예측하는 선형회귀 식이 아래의 빨간색 직선으로 구성되었다고 가정하자.
 

 
이를 각 데이터 포인트와 선형회귀식으로 구한 $\hat{y}$ 로 부터 잔차 그래프는 다음과 같이 얻을 수 있다.
$residual =  y - \hat{y}$
 

 

보이는 그래프는 Predicted value $\hat{y}$의 값에 상관없이 Residual이 고르게 퍼져있는 모습으로, 등분산의 형태를 띄고 있음을 알 수 있으며, 이는 2번째 성질은 "잔차의 등분산성"에 해당한다.

여기서 만약 현재의 그래프에서 잔차를 $x$축으로 하여 그래프로 표현하고자 한다면,
아래와 같이 평균이 0이고 분산이 1인 형태의 정규 분포의 형상을 띌 것이고, 이는 3번째 성질인 잔차의 정규성 가정을 만족하는 것을 알 수 있다.
 

 
 
 
그러나 만약 원래의 target distribution이 아래와 같이 정규 분포가 아닌 오른쪽이나 왼쪽으로 치우친 형태의 분포라면 잔차의 분포가 이상적인 정규 분포에서 벗어날 가능성이 높게 된다.

Ames시 집 값의 분포(https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques)

 
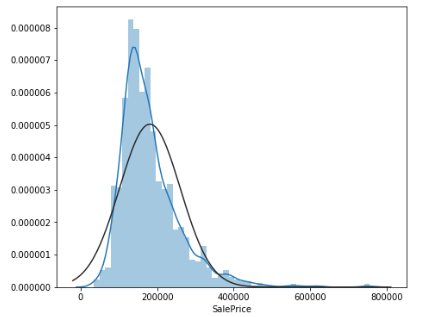
일반적인 데이터에서 자주 관찰되는 오른쪽으로 긴 꼬리 분포(right-skwed)의 경우,  데이터의 극단적인 값(본 예시에서는 비싼 집값)이 오른쪽에 분포함을 나타낸다. 이러한 분포의 경우, 극단값에서 발생하는 잔차와 중앙값 근처에서 발생하는 잔차의 스케일에는 큰 차이가 발생하게 되고, 잔차의 분포 역시 타겟의 분포와 비슷한 경향을 보일 수 있다. 
 
 

② Feature $X$ Distribution

데이터 포인트의 피처를 로그 변환 혹은 박스 콕스 변환을 통해 정규성을 확보하는 목적은 정규성 보다는 스케일에 있다.
로그 변환이나 박스콕스 변환을 거치게되면 잔차의 분산도 작아지게 되며, 극단값에 대한 민감도 역시 줄어 들게 된다. 

https://recipesds.tistory.com/entry/%EB%8D%B0%EC%9D%B4%ED%84%B0%EB%A5%BC-%EB%A1%9C%EA%B7%B8-%EB%B3%80%ED%99%98-%ED%96%88%EC%9D%84-%EB%95%8C-%EB%B2%8C%EC%96%B4%EC%A7%80%EB%8A%94-%EC%9D%BC%EA%B3%BC-%EA%B2%B0%EA%B3%BC-%ED%95%B4%EC%84%9D

 

로그 변환은 데이터의 이상치(outliers)가 모델에 미치는 영향을 줄여주며, 모델이 데이터의 중심부에 더 집중하게 되어, 극단적인 값들에 의한 왜곡을 줄일 수 있고, 변환 과정에서 극단값의 상대적 영향력이 감소하기 때문이다.
 
 

결론

 

선형모델의 4가지 가정은 애당초 선형모델이 그러한 가정으로 부터 출발하여 만들어졌기 때문에 발생한 것으로, 가정이 지켜져야 올바른 선형모델이 될 수 있다.

 

물론, 가정이 지켜지지 않는다고 해서 선형모델을 피팅할 수 없는 것은 아니다. 하지만 모델의 계수(coefficient)를 신뢰할 수 있는가의 문제에는 긍정을 하기 어렵다.

 

결론적으로, 로그 변환은 이러한 장점들 덕분에 선형 회귀 모델, 일반화 선형 모델 등 다양한 통계적 모델링 방법에 적합하게 만드는 데 효과적인 방법이다. 하지만, 역시나 모든 데이터 피처 집합에 대해 로그 변환이 꼭 유용한 것은 아니므로, 변환을 적용하기 전에 데이터의 특성과 모델링 목적을 반드시 고려해야만 한다.

 

선형 모델의 4가지 성질에 대한 이야기는 수식이 반드시 함께 동반되어야 함으로, 다음 글에서 이어가도록 하겠다. 
 
 
 

---

Reference)
https://recipesds.tistory.com/entry/%EB%8D%B0%EC%9D%B4%ED%84%B0%EB%A5%BC-%EB%A1%9C%EA%B7%B8-%EB%B3%80%ED%99%98-%ED%96%88%EC%9D%84-%EB%95%8C-%EB%B2%8C%EC%96%B4%EC%A7%80%EB%8A%94-%EC%9D%BC%EA%B3%BC-%EA%B2%B0%EA%B3%BC-%ED%95%B4%EC%84%9D
https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques