EECS 498-007 Lecture10: Training Neural Networks Part1 정리

 

 

Neural Net을 학습시킬때 고려해야 할 요소들에 대해서 알아본다. 

 

 

Neural Net을 학습시킬때는  학습 사전에 결정되어 진행되는 것들이 있고

Learning rate schedule과 같이 학습중에 동적으로 변동되는 것들이 있으며

훈련이 모두 마친후 모델 앙상블, 혹은 전이학습(Transfer Learning)과 같이 좀 더 downstream task로 나아가는 방법이 있다.

 

 

첫번째로 알아볼 것은 활성화 함수(Activation Function)이다.

 

 

NeuralNet에서 활성화 함수로서 선택할 수 있는 대표적인 선택지이다. 디테일에 대해서는 지난시간 내용을 다시 참고하길 바란다.

 

 

 

학습시 Acitvation Function을 Sigmoid함수로 설정했을때의 기능에 대해서 알아보자.

Sigmoid함수는 input의 로짓값을 [0,1] 범위의 값으로 대치한다.

ouput scalar로부터 마치 뉴런의 활성화 정도, 뉴런의 firing rate로 이해할 수 있게한다.

 

그러나 Sigmoid함수의 사용시 문제는 input logit값이 양 극단으로 갈경우 'gradient saturation'문제가 생긴다. saturated된 뉴런들은 gradient의 정보들을 모두 파괴한다.(0에 수렴해간다.) 즉, Backpropagation시 gradient의 전파는

 

downstream gradinet = local gradient * upstream gradient에서 local gradient가 0에 가깝기 때문에 전파되는 downstream gradient역시 0에 가까워져 신경망을 더 깊이 만들수록 학습에 지장을 초래하게 된다.

 

 

Sigmoid를 활성화함수로 사용했을 시, 두번째 문제는 시그모이드의 결과출력값이 zero-centered가 아니라는 점이다.

Sigmoid의 출력값은 모두 0초과, 1미만의 양수값만을 가지게 된다.

 

이렇게 되는 것이 어떤 문제가 있을까?

 

 

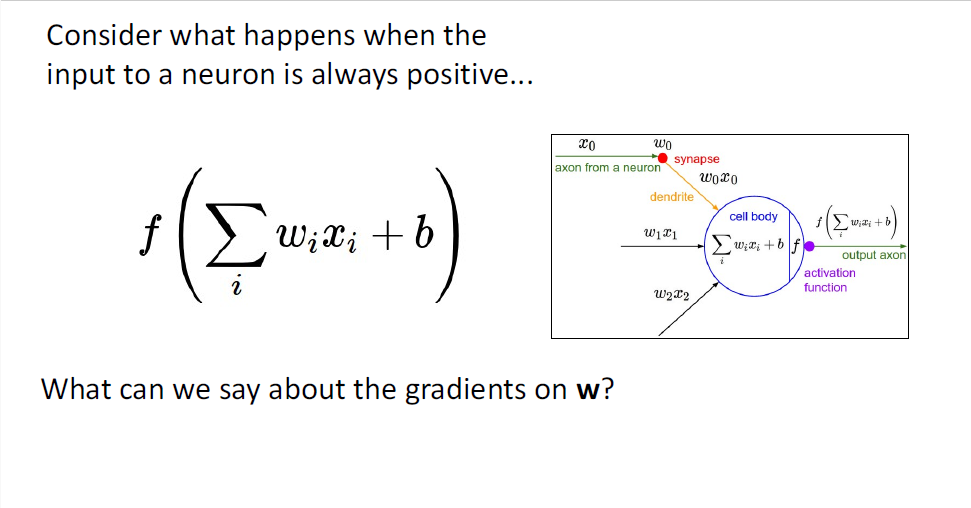
만약 뉴런의 인풋값이 항상 양수로만 세팅된다고 가정하자, 이때 인풋값은 $x_i$를 의미할 것이고, 뉴런의 가중치와 bias에의해 어떠한 값으로 변환되고, 변환된 값에 대하여 활성화 함수 $f$가 적용되는 것이 어떤 인공신경망의 뉴런 연산이다.

 

이러한 과정에서 가중치 $w$의 gradient에 대해서 무어라고 말할 수 있을까?

 

만약 모든 뉴런으로 들어오는 input값이 양수라는 제약조건을 가지게 되면, 

가중치 $w$가 그림과 같이 어떤 2차원의 형태라고 한다면, 업데이트 되는 방향이 특정한 두개의 사분면에 국한될 수 밖에 없게 된다.

 

downstream gradient = local gradient * upstream gradient에서 모든 local gradient($\frac{\partial {L}}{\partial {W_i}}는

$x_i$가 되어 모든 local gradient가 양수가 된다.

이상황에서 upstream gradient는 단순히 scalar의 역할만을 수행하여

downstream gradient는 upstream gradient가 음이면 모두 음수, 양수면 양수로 결정되게 된다.

 

따라서 업데이트를 통해 특정 값에 도달하기 위한 가중치 벡터 $w$는 그림 과 같이 지그재그 패턴을 보일 것이다. 

 

 

 

 

 

 

위의 그림은 2차원이라서 지그재그 패턴이 큰 문제가 아니라고 생각될 수 있는데, 가중치 $w$는 매우 고차원인 것이 일반적이기 때문에, 이러한 상황에서 지그재그 패턴은 더욱 심각해져 간다.

 

 

 

 

시그모이드의 세번째 문제는 exponential 연산의 연산량이 많다는 점이다.

 

 

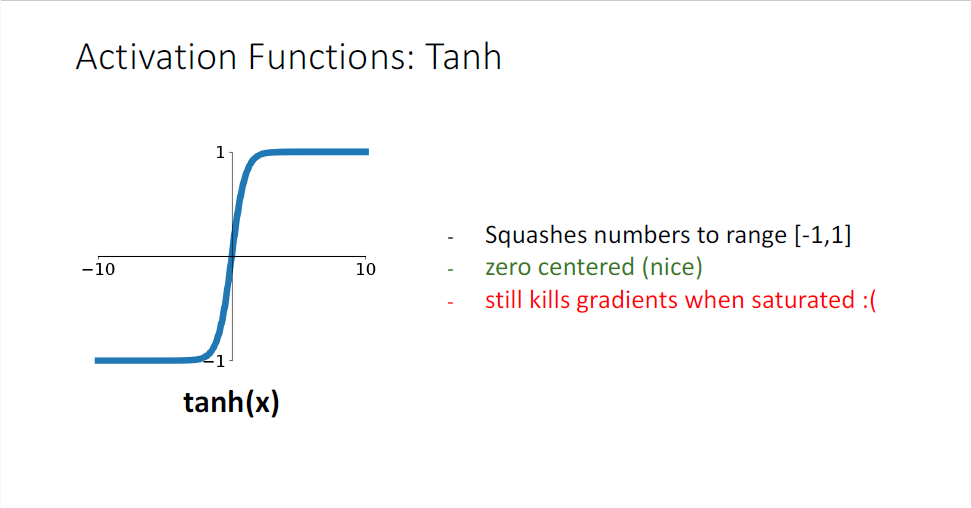
다음으로 tanh(x) (하피어볼릭탄젠트)이다. (0,1)의 범위가 아니라 (-1,1)의 범위로 대치한다.

이에 따라 output은 zero-centered이기 때문에 업데이트의 방향에 관해 좀 더 나은 성질을 갖는다.

그러나 여전히 satruated될 때 gradient vanishing이 발생한다.

 

 

ReLU함수는 input이 어떤 값이 들어와도 gradient saturation이 발생하지 않는다.

또한 단순히 0 또는, 원래의 input값을 선택하는 1회의 max연산이기 때문에 연산량이 매우 적다.

또한 시그모이드와 하이퍼볼릭탄젠트보다 6배 빠른 수렴속도를 보인다.

 

 

그러나 ReLU역시  zero centered가 아닌 문제가 있다. 

 

 

 

또한 음수 값을 0으로 죽이기 때문에 이부분의 gradient 소실에 관한 문제가 있을 수 있다.

 

ReLU의 input값이 0보다 작게되면 gradient가 0이되어 학습이 전혀 진행되지 않게 된다. 

sigmoid함수의 경우에는 input값이 매우 크거나 매우 작다하더라도 일정 부분의 매우 작은 gradient로 학습에 대한 기대를 걸 수 있지만 ReLU는 아예 gradient가 0으로 완전히 죽기 때문에

이러한 부분은 sigmoid함수보다 낫다고 할 수 없는 점이다. 

 

 

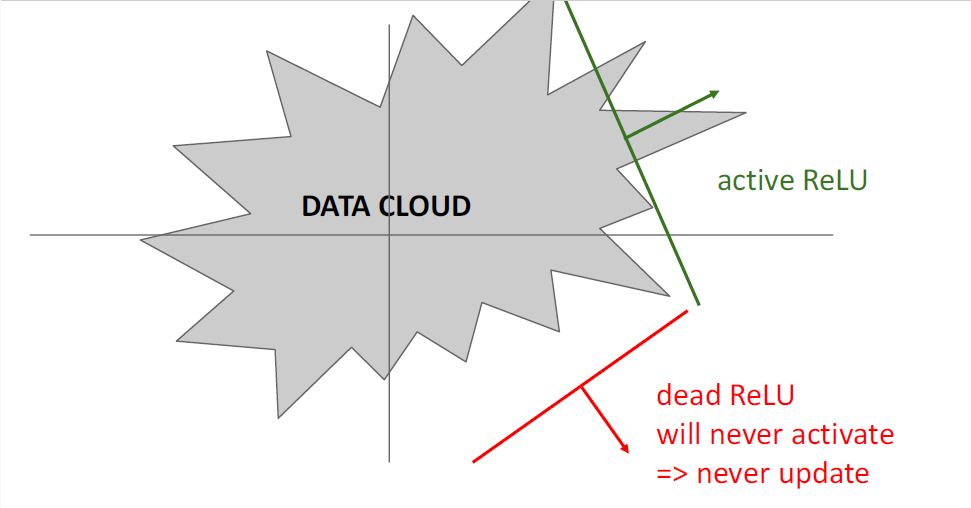
사람들이 걱정한 이러한 문제를 "Dead ReLU"라고 부른다.

 

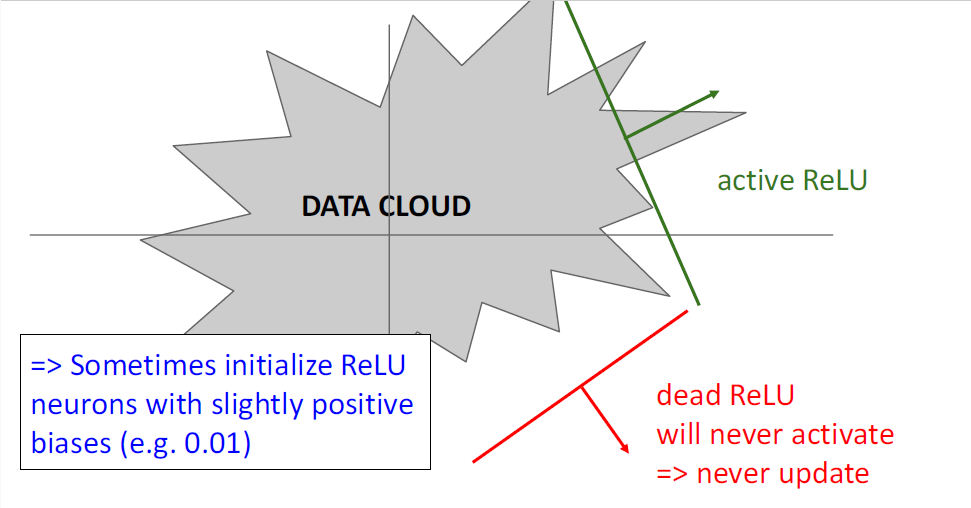
사람들은 이러한 문제를 피하기 위해, 즉 ReLU에 양수값의 input을 넘겨주기 위해 ReLU에 매우 작은 bias를 주는 방식을 취하기도 하였다.

 

 

ReLU의 두가지 큰 문제는 not zero-centered라는 것과 음의 영역에서 zero gradient라는 것인데 

두가지 문제를 모두 해결한 것이 바로 Leaky ReLU이다.

양수의 영역에는 ReLU와 동일하게 1의 gradient를 갖지만, 음의 영역에서는 매우 매우 작은 양의 gradient값을 갖게 된다.

따라서 ReLU에서 정보의 조그마한 부분의 leaks, 새나갔다고 표현하여 Leaky ReLU라고 부르게 되었다.

 

음수의 영역에 gradient(현재는 0.01)은 하이퍼파라미터로서 튜닝할 수 있는 부분이다.

 

Leaky ReLU의 장점은 ReLU와 같이 saturation문제가 발생하지 않으며

단 두 연산으로 매우 연산량이 적고

시그모이드나 ReLU처럼 dying현상이 발생하지 않는다.

 

하이퍼 파라미터는 결국, 모델의 학습에 있어서 선택사항을 추가하는 것으로

학습을 더욱 복잡하게 만드는 요소인데

하이퍼 파라미터라고 소개했던 부분을 learnable parameter로 만드는 PReLU도 있다.

 

그러나 아직 짚지 않은 한가지의 문제가 있는데 바로 $x=0$에 관한 것이다.

$x=0$에서 ReLU는 미분가능하지 않은데, 실제로는 매우 작은 gradient값을 부여하기도 하는데 입력값이 0인 경우는 거의 잘 없기 때문에 큰 고려대상은 아니다.

 

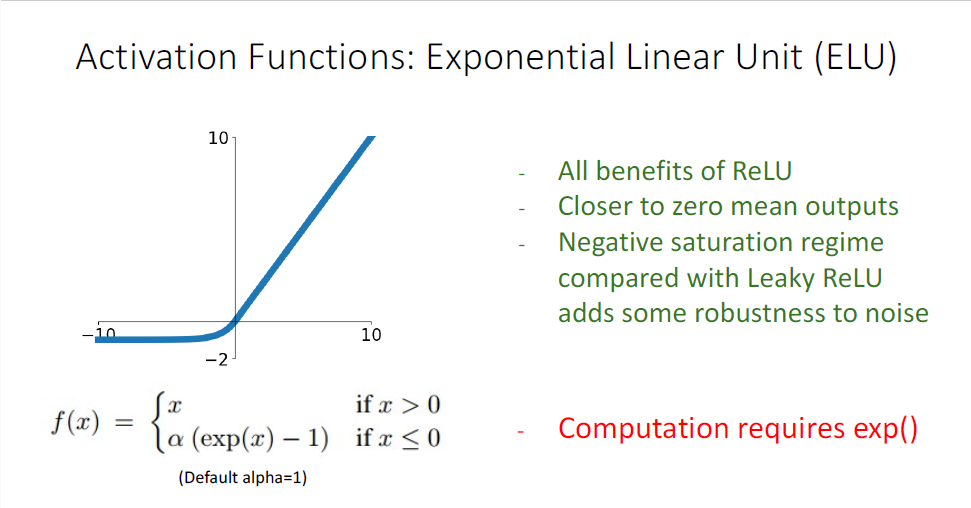
다음으로 살펴볼 것은 ELU이다. 역시 ReLU의 문제를 해결한 버전이다.

ReLU와 비슷한 함수이지만 zero-centered이다. 하지만 함수의 정의에서 보듯이 exponentail value에 대한 연산이 필요하다. 또한 $\alpha$를 PReLU처럼 learnable parameter로 학습할 수 있지만, 실제로 그렇게하는 경우는 거의 잘 없다. (Default alpha=1)

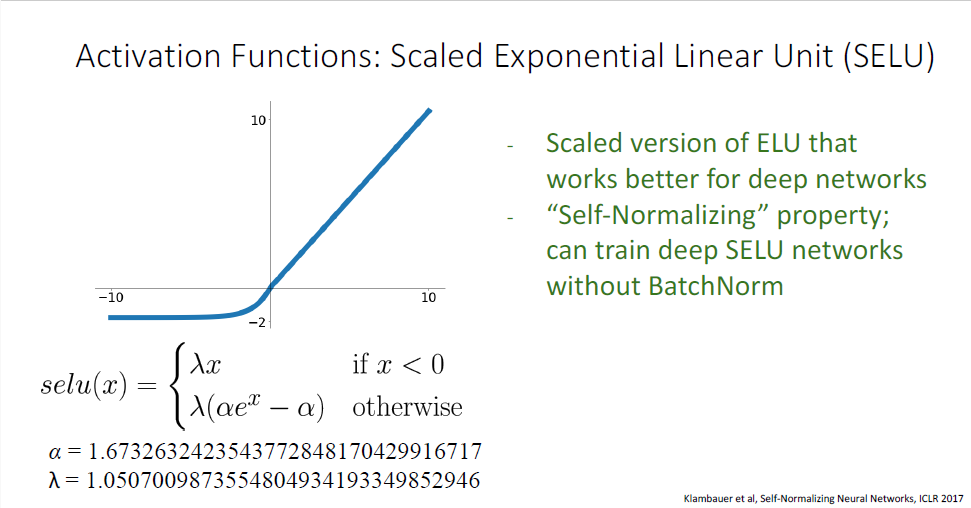
비선형 함수들은 사실 매우 작은 모듈에 불과하기 때문에 NeuralNet 시스템 전체에 대해 적용해보고, 실험하여 변화를 관찰하려는 시도들이 많이 있었고 실제로 많은 발표들이 있었다.

 

흥미로운 발표중에 하나가 SELU인데, SELU는 이전 슬라이드의 ELU의 rescale버전이다. $\alpha$와 $\lambda$를 매우 긴 형태의 상수 값으로 사용한다. 

 

특별히 매우 Deep한, 매우매우 Deep한 NeraulNetwork에 SeLU를 적용하면 Self-Normalizing의 속성을 갖게되어, BatchNorm등을 사용하지 않아도 수렴이 잘 된다고 한다.

 

이러한 현상을 이해하기 위해선 91페이지에 달하는 appendix 페이지를 읽어야한다... 대단한 참을성이 있다면 왜 저렇게 특별한 상수값을 채택했는지 이해해볼 수 있을 것이다... 

 

지금까지 많은 ReLU의 변형들에 살펴보았는데, 실제로는 이러한 다양한 버전들에 대해서 큰 성능차이가 없다.

 

 

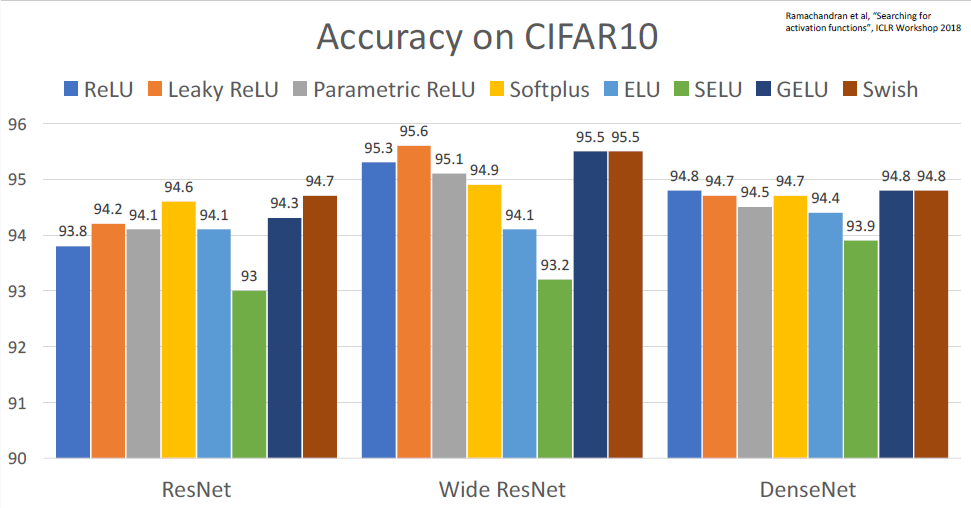
CIFAR-10 데이터셋을 이용한 다양한 아키텍쳐에 따른 실험 결과이다.

결론은 Sigmoid나 tanh를 제외한 Modern non-linearity(비선형 활성화함수)를 사용하라.

Dataset이나 모델 아키텍쳐에 따라 1~2%정도의 정확도 차이가 날수도 있지만, nonlinearity에 대해서 처음부터 큰 고민할 필요는 없다.

 

추가적으로 지금까지 살펴본 모든 함수들은 단조의 함수인데, 왜 코사인과 사인함수와 같이 단조적이지 않은 함수를 활성화함수로 채택하지 않는가에 대한 질문이 있다.

사실 다루지 않은 GeLU가 있어서 약간의 거짓말이 될수도 있는 답변인데,

만약 사인과 코사인함수와 같은 비단조 함수(non-monotonic)을 사용하면 하나의 output $y%에 대해 여러개의 $x$값이 존재할 수 있다. 이렇게 되면 학습에 있어 문제를 겪게된다. 활성화 함수가 역함수를 가지지 않는다면 정보를 잃게 된다.

 

Activation function의 목적은 단지 계산을 편리하게 하기 위한 용도가 아니라, 신경망의 전체 시스템에 비선형성(nonlinearity)를 추가하는 것임을 잊지 말아야한다. 활성화함수를 사인이나 코사인함수를 채택하여 NeuralNet을 학습시킨 경우도 보긴 했는데, Batch Normalization등을 매우 적절히 사용해야 겨우 학습이 될것인데 이를 추천하지는 않는다.

 

특별히 GeLU에 대해서 이야기 하자면, GeLu논문을 반드시 읽어보기를 추천하며, GeLU의 non-monotically한 속성은 약간의 regularization으로 해석된다.

(각주: 강의에서는 non-monotonic한 함수는 잘 사용되지 않고 대부분 단조함수인 활성화 함수가 사용된다고 했는데, 24년 기준으로는  Activation function에서 아마도 GeLU가 단연 압도적일 것이다.)

 

 

다음으로 살펴볼 것은 Data Preprocessing이다.

 

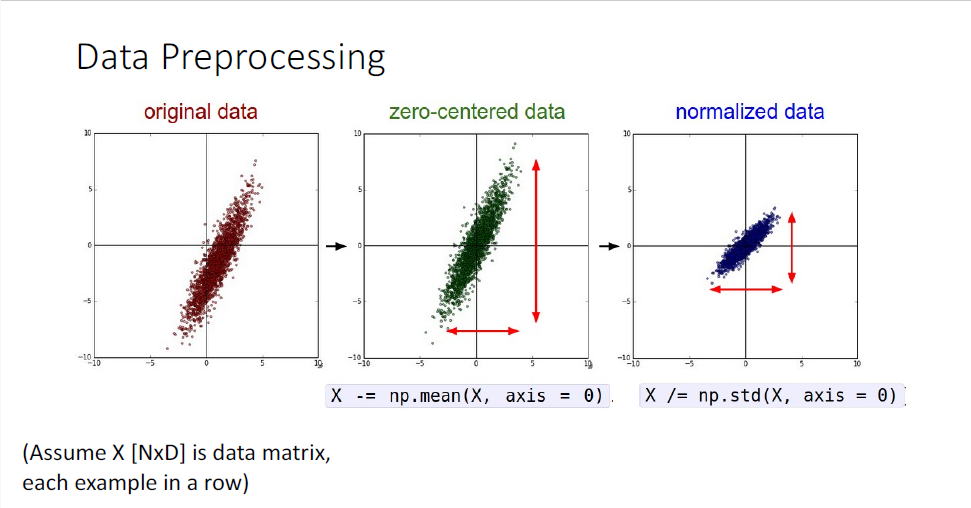
Data Preprocessing은 우리가 신경망에 input으로 주기 전에 데이터의 분포를 바꿔주는 것으로,

일반적으로 이미지를 다룬다고 한다면, 이미지 픽셀이 0~255로 구성되어 있기 때문에 이들 값은 원점(origin)으로부터 대단히 멀리 떨어져 있다는 것을 안다. 따라서 데이터를 normalizing하여 신경망의 입력으로 사용하게 된다.

 

 

우리가 데이터를 normalizing하는 것은 sigmoid nonliearity에서 보았던 zero centered의 특징으로인해 발생한 zig-zag problem과 비슷한 맥락이다. sigmoid에서 보았듯 input이 모두 양수이거나 음수이게되면 output역시 여전히 모두 양수이거나 음수인 문제가 발생하였는데, 마찬가지의 논리로 데이터가 모두 양수값이면 모두 양이거나 모두 음인 하나의 부호만을 갖게 되는 제약이 발생하게 된다. 그러나 traning data는 단순히 rescale함으로써 이러한 문제를 개선할 수 있다.

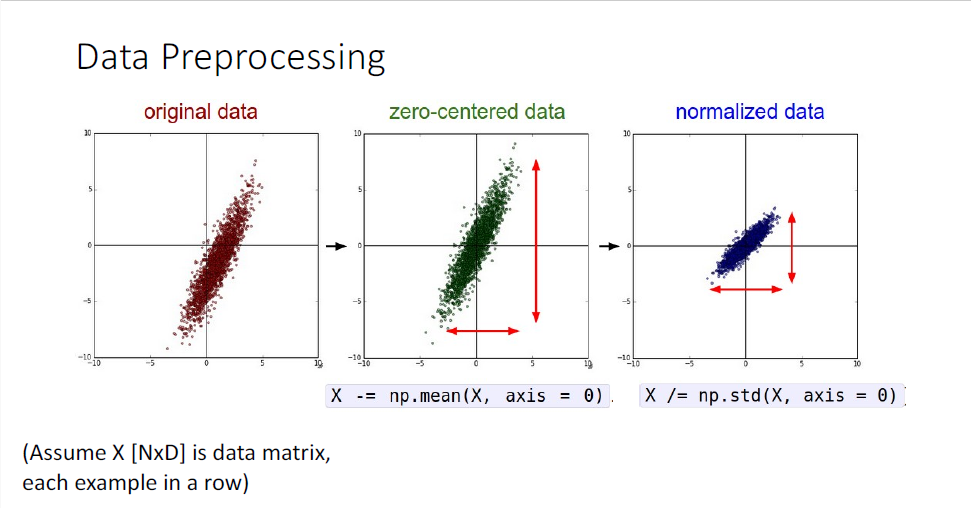
단순히 이미지 데이터는 평균을 빼고 표준편차를 나눠주는 것으로 rescaling을 해주는 경우가 많은데

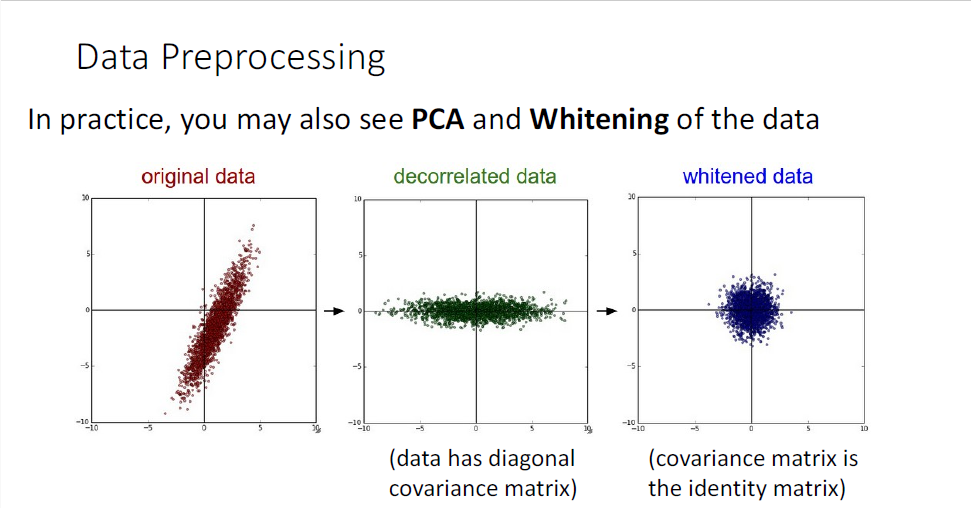
다른 타입의 데이터 같은 경우에는  PCA혹은 Whitening이라 불리는 다른 data preprocessing의 종류도 있다.

이들의 아이디어는 만약 traning set으로부터 공분산 행렬(covariance matrix)를 계산할 수 있다면,

가운데 초록색 그림처럼 data cloud를 회전시켜 uncorrelated의 형태로 만들어 사용하거나

이후 각각 개별적인 feature에 대해 zero mean, unit variance로 통일하게 되어 가장 우측 파란색 그림처럼 구의 형태를 띄는 데이터의 분포로 만들어 이를 사용하는 whitening이 있다.

 

이러한 데이터 전처리 기법은 전차원의 벡터 형태일 경우 유효한 기법이지만, 이미지 데이터같은 경우에는 일반적으로 사용하지 않는다. (이미지는 매우매우 고차원의 feature vector이기 때문에 역행렬 계산과 공분산 행렬 계산이 사실상 불가능하다.)

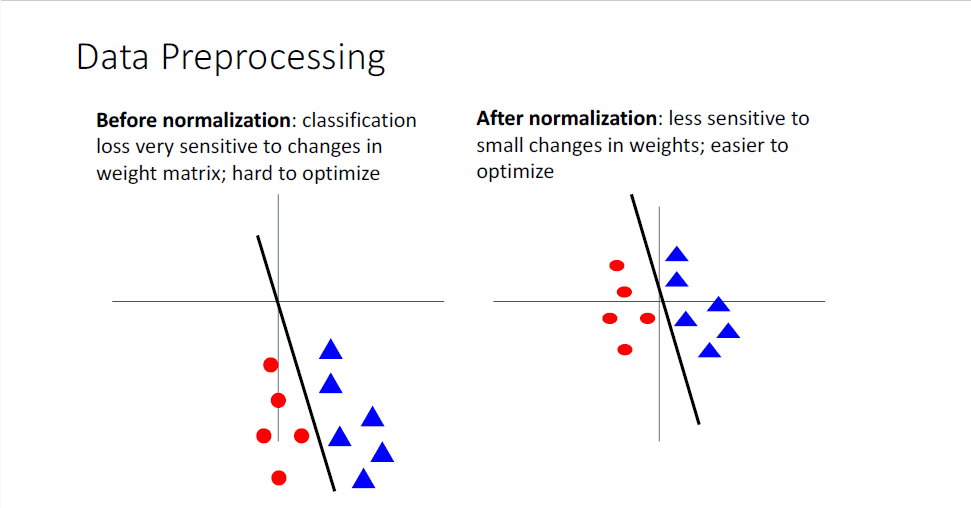
데이터 normalizing이 왜 유효한 방법일까?

non standardized data를 Linear Classifier에 적용시키는 예시를 통해 알아보자.

 

좌측 그림의 데이터는 원점으로부터 멀리 떨어져 있고, 우측의 데이터는 noramlized되어 원점에 매우 가깝게 위치한다.

좌측에서는 Linear Classifier의 경사(slope)를 조금만 틀어도 분류가 매우 부정확해진다.

그러나 우측의 Linear Classifier는 경사의 조금의 변화에도 강건한 형태이다.

 

즉 좌측의 경우, $W$ Matrix의 작은 변화에도 decision boundary가 매우 민감하게 변하게 되는 것이다.

그러나 data를 normalizing하게 되면 optimizatinon이 더 쉬운 상태라고 말할 수 있다.

 

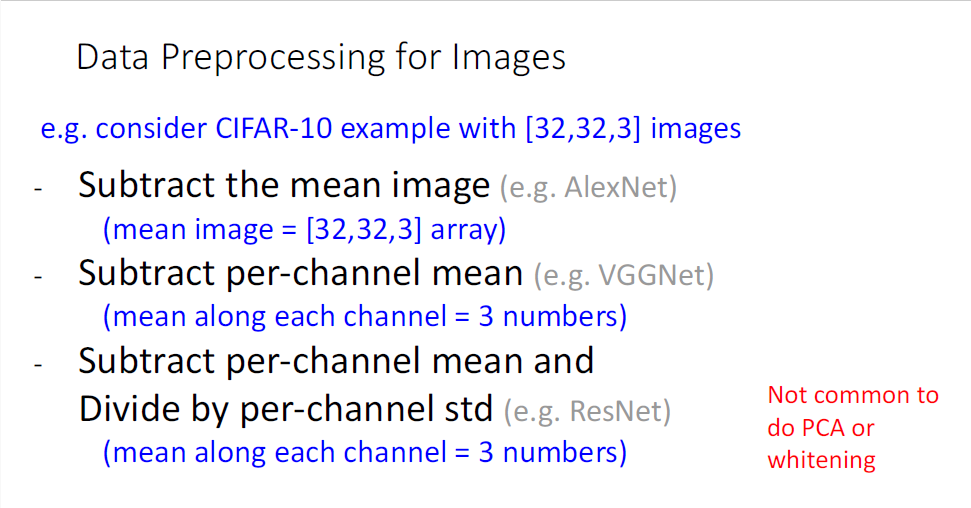
이미지 데이터의 pre-processing은 일반적으로 위의 세가지 방법을 사용하며, test단계에서는 traning dataset의 평균과 표준편차의 정보를 이용하게 된다.

그렇다면 Batch Normalization을 사용하는 경우에도 이러한 normalization 테크닉을 적용해야되는가? 의문이 들 수 있다.

정답은 그렇다. pre-processing을 하여도 Batch Normalization은 작동한다. 네트워킈 가장 앞단의 convolution layer나 fc layer에 Batch Normalization을 적용하여도 실제로 잘 작동한다.

 

다음으로 살펴볼 것은 가중치 초기화(Weight Initialization)이다.

 

 

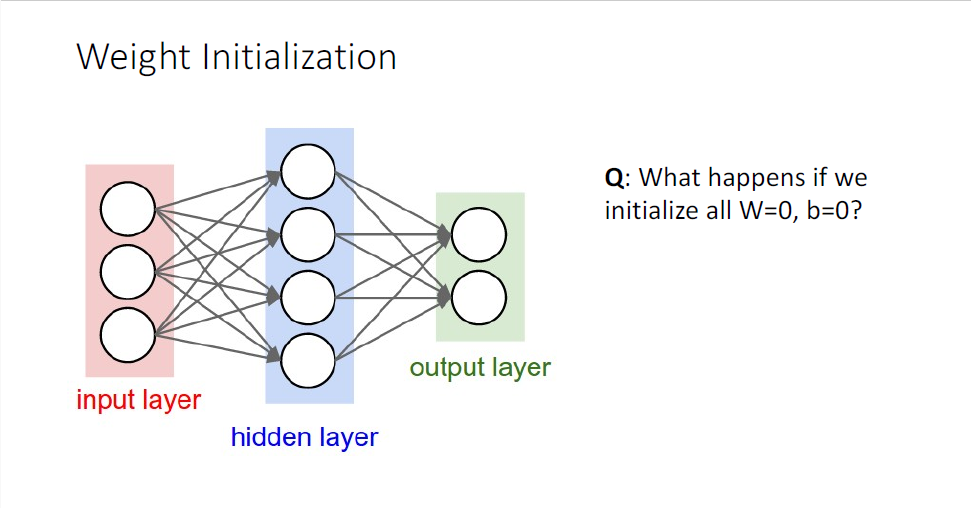
학습 과정에서는 반드시 가중치의 초기값이 필요한데, 만약 모든 가중치와 bias가 0이면 어떻게 될까?

 

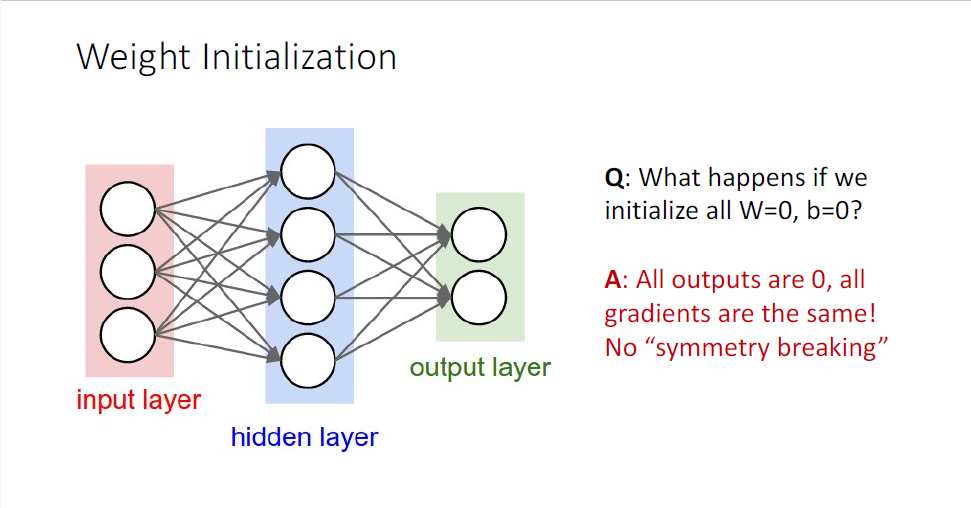
모든 oupput이 0이고 모든 gradient가 0이기 때문에 어떠한 학습도 일어나지 않을 것이다. 0뿐만 아니라 가중치를 동일한 특정 상수로 초기화를 하더라도 동일한 output과 동일한 gradient를 갖기 때문에, 'symmetry breaking'이라고 불리는 구분현상을 발생시키지 않기 때문에 학습이 일어나지 않는다.

 

처음의 아이디어는 간단히 작은 값으로 초기화 하는 방법으로

zero mean과 std=0.01의 가우시안 분포로 초기화하는 방법이다.

 

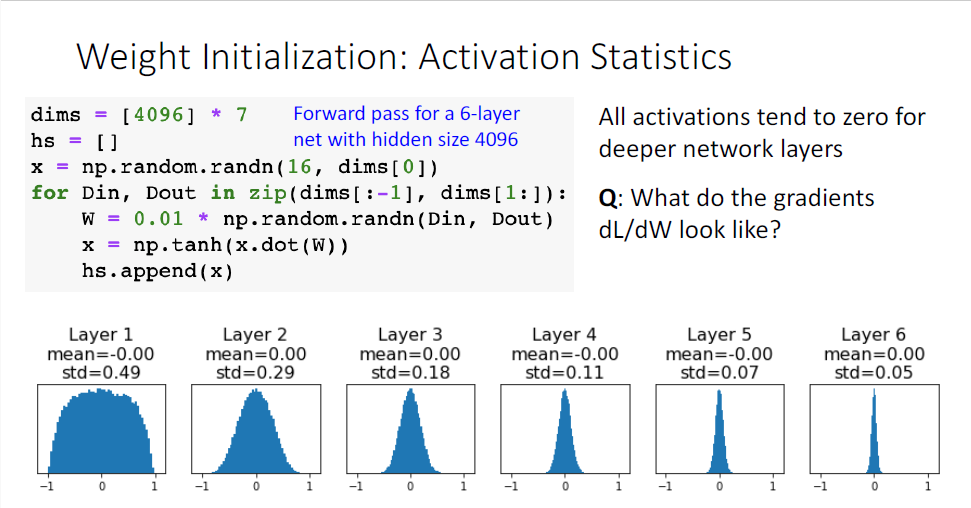
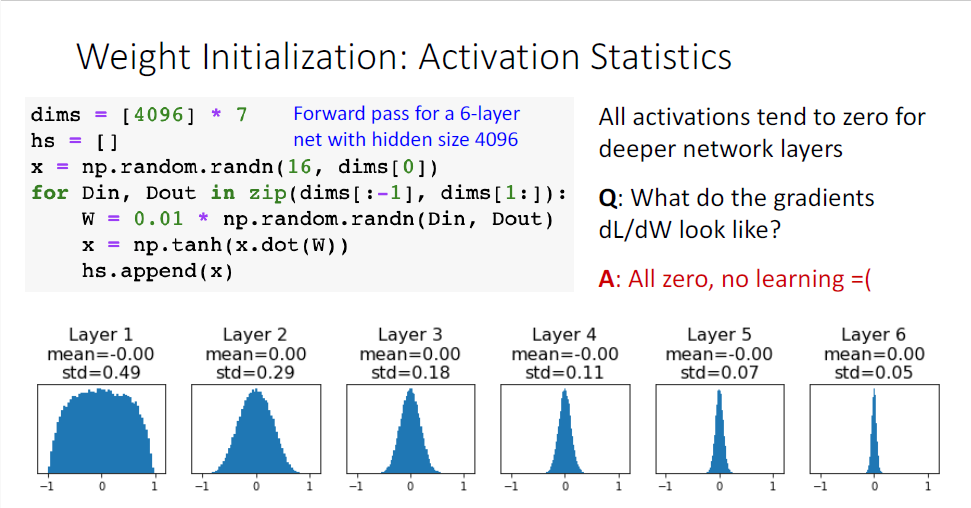
그러나 이 방법은 shallow 네트워크에서는 잘 작동하지만 deep한 네트워크에서는 잘 작동하지 않게 된다.

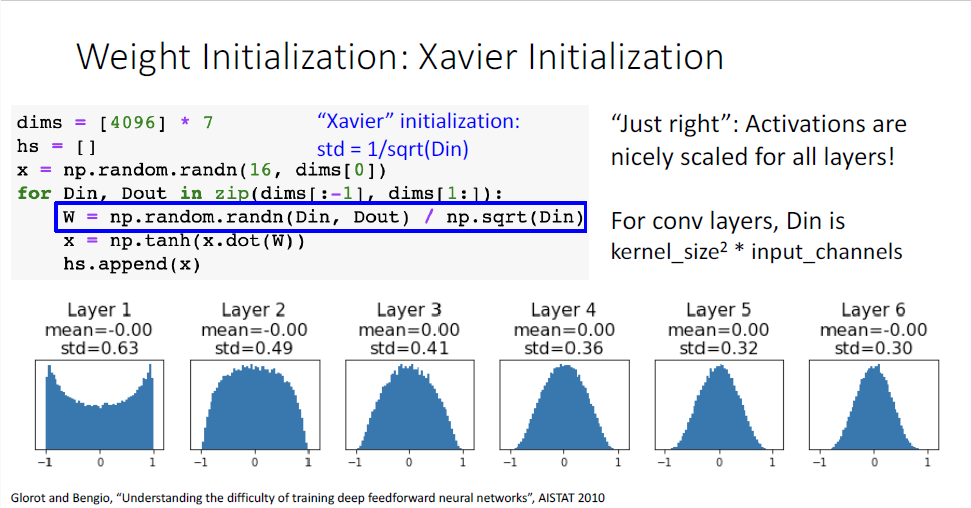
6개의 레이어에 대한 예시 코드이다.