플로라도의 data workout

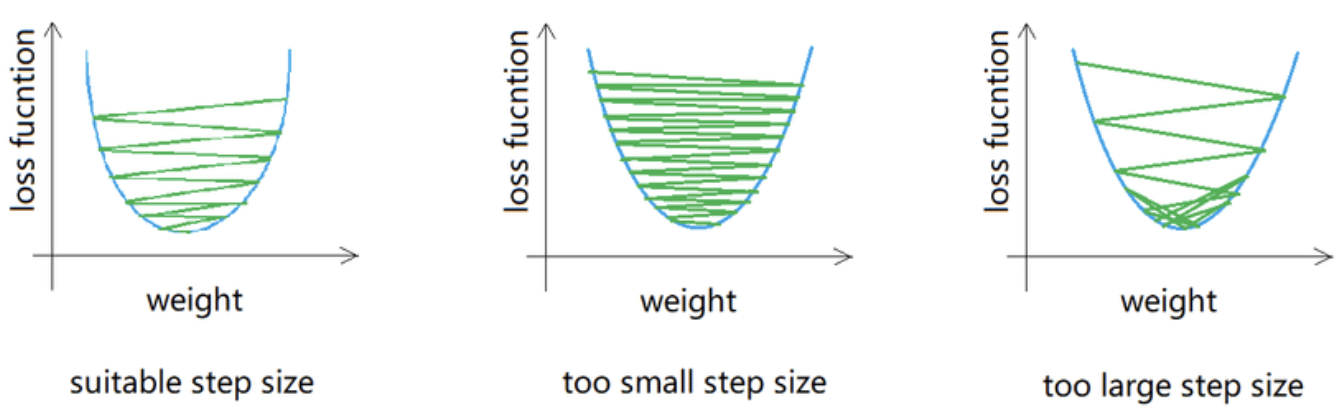
Claim1) 뉴턴 랩슨의 방법은 두 번 미분하는 과정이 필요하다. 계산량이 많다. 경사 하강법이 더 일반적이다!? 수업시간에 들었던 이야기다. 경사하강법과 뉴턴-랩슨의 방법에 대한 정리와 함께 Claim1에 대한 이해와 해결을 해보려고 한다. 경사하강법(graident decent)와 뉴턴 랩슨의 방법(Newton-Raphson method)는 모두 기계학습의 Learning Rule에 해당하는 이야기 이다. 모델이 어떻게 파라미터를 최적화 시키도록 할것인가? 지시하는 Rule이라고 할 수 있겠다. 머신러닝의 가장 기본적인 모형인 선형회귀와 로지스틱회귀를 생각해보자. 선형회귀에서는 비용함수를 최소화 하는방법으로 기본적으로 (1)정규 방정식, (2)경사하강법을 사용하게 된다. 로지스틱회귀(Logistic..

어떤 x,y가 위와 같은 2차원 유클리드 공간에 속하는 녀석이라고 하자. 일변수 스칼라 함수 e.g. - $y=x^2$ , $y=cos(x)$, $y=e^x$, $y=log(x)$ - 우리가 잘 아는 다항함수 뿐만 아니라, 삼각함수,지수함수,로그함수 등의 초월함수도 포함된다. 일변수 스칼라 함수는 {x} -> {y} 로 대응 되는것을 표현하는것인데, 이 '대응'이라는 것은 다시 말해, 독립변수 $x$가, 종속변수 $y$로 어떤 함수 $f$ 에 의해서 매핑 되는 것 이라고 생각하면 된다. 즉, 독립변수 $x$가 종속변수 $y$로 매핑되는 것이다. 일변수 벡터 함수 일변수 벡터함수는 일변수 스칼라 함수와 다르게 입력값이 일변수인것은 같지만 출력이 여러개로 나타난다. {t} -> {x,y,z} 로 대응이 된다..

보통 우리가 확률을 이야기 할때, 주사위 던지기 게임, 동전던지기 게임을 예시로 많이 든다. 가장 명료하면서도 확률의 여러 개념들을 포괄하는 예시이기 때문이다. 가장 처음에, 누구에게나 하는 질문이 이거다. 주사위를 던졌을 때 주사위 눈이 1이 나올 확률은 몇일까? 보통은 이렇다, "잘 알고 있듯이 1/6입니다. 여러분은 확률을 잘 알고 있습니다~" 우리가 지금껏 배워왔던 대부분의 확률은 이러했고, 우리는 확률과 아주 친숙함을 주입되어왔다. 그런데, 정말 주사위 1의 눈이 나올 확률이 1/6이라고 보장 할 수 있을까? 사실은, 주사위에 누군가 임의의 조작을 걸어서 정육면체의 큐브형 주사위가 아니라 '1'의 면이 울퉁불퉁해서 다른면 보다 덜 나오게 세팅이 되었다고 한다면.. 그래도 1/6이라고 말 할 수 ..