Bias-Variance Decomposition은 머신러닝 모델의 일반화 오차(generalization error)를 분석하는데 사용되는 개념이다.
이는 오차를 세가지의 요소로 분해한다.
1. Bias(편향)
모델(estimator)의 예측(estimate)과 실제 값(target) 사이의 차이를 말한다. 모델이 학습 데이터에만 과도하게 맞춰진 오버피팅 상태에서 편향이 발생한다.
2. Variance(분산)
모델의 예측(estimate)의 변동성을 나타낸다. 모델이 학습 데이터에 언더피팅된 상태에서 분산이 증가하게 된다.
3. Noise(노이즈)
데이터 자체의 내재적인 불확실성이다. 모델이 제거할 수 없는 에러나 데이터 발생시 불특정한 이유에서 발생한 에러를 의미한다. 노이즈의 발생 원인은 다양할 수 있으며, 측정 오류나 데이터 수집 과정에서 환경적인 요인의 변동 등을 개념적으로 포함한다.
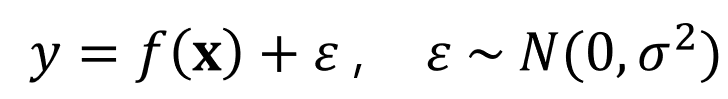
이러한 가정에서 노이즈는 평균이 0이고 분산이 $\sigma^2$인 i.i.d(independent and identically distributed)로부터 샘플링 되었다고 가정한다. 위의 식에서 $f(x)$는 우리가 찾고자 하는 true function이며, 우리의 모델 $\hat{f(x)}$는 true function $f(x)$를 모사하도록 하는 것이 목표이다.
타겟 값 $y$로 부터 노이즈 $\epsilon$을 분해하기 쉽지 않기 때문에, 우리가 머신러닝을 통해 모델링 함수 $\hat{f(x)}$를 true function $f(x)$로 근사하는 일이 쉽지 않음을 이야기 하고 있다.


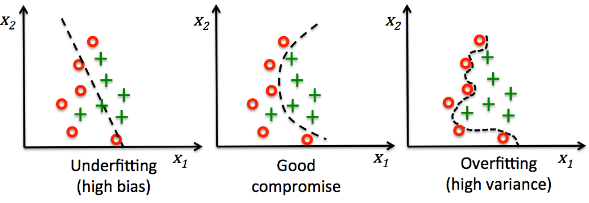
Bias와 Variance에 따른 모델의 예측값(파란점)과 타겟값(빨간원)과의 관계를 나타낸다.
전체 Error는 Bias^2 + Variance로 표현될 수 있으며 모델의 복잡도(Model Complexity)가 커짐에 따라 일반화 오차의 양상을 보여준다. 따라서 적절한 모델 복잡도를 선택하는 것이 매우 중요하다.
Linear Model에서는 Bias와 Variance의 상태를 다음과 같은 그림으로 표현할 수 있다.

두가지 범주를 분류하는 Binary Classifier의 Bias와 Variance는 다음과 같은 그림으로 표현할 수 있다.
Bias-Variance Decomposition
일반적으로 MSE(Mean Sqared Error)는 아래의 식처럼 추정치 $\hat{\theta_s}$과 타겟 $\theta$와의 차의 제곱의 평균을 의미하는데,
Bias^2는 모델(estimator)의 예측(estimate)과 실제 값(target) 사이의 차이의 제곱을 의미하고,
편차의 제곱의 기댓값을 의미하는 Variance는 제곱의 평균에서 평균의 제곱을 뺀 값과 동일하다.
따라서 Bias^2 term과 Variance term을 모두 더하면 MSE값과 동일함으로
MSE가 Bias^2과 Vairnace로 Decompoistion됨을 알 수 있다.

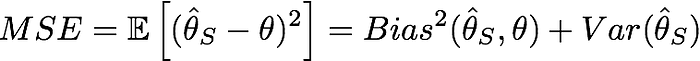
Reference
https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote12.html
'기초 노트 > DataScience' 카테고리의 다른 글
| 차원의 저주(Curse of dimensionality) (0) | 2024.03.07 |
|---|---|
| Stacking과 Blending의 차이 설명 (5) | 2024.03.06 |
| 원-핫 인코딩의 모든 것(feat.OneHotEncoder vs pd.get_dummies) (1) | 2024.03.05 |
| Loss Function vs Cost Function vs Objective Function은 무슨 차이 인가요? (0) | 2023.07.01 |
| 경사하강법 (gradient desecent) vs 뉴턴-랩슨 방법 (Newton–Raphson method) (0) | 2023.07.01 |