플로라도의 data workout
경사하강법 (gradient desecent) vs 뉴턴-랩슨 방법 (Newton–Raphson method) 본문
경사하강법 (gradient desecent) vs 뉴턴-랩슨 방법 (Newton–Raphson method)
플로라도 2023. 7. 1. 12:35
Claim1) 뉴턴 랩슨의 방법은 두 번 미분하는 과정이 필요하다.
계산량이 많다. 경사 하강법이 더 일반적이다!?
수업시간에 들었던 이야기다.
경사하강법과 뉴턴-랩슨의 방법에 대한 정리와 함께 Claim1에 대한 이해와 해결을 해보려고 한다.
경사하강법(graident decent)와 뉴턴 랩슨의 방법(Newton-Raphson method)는 모두 기계학습의 Learning Rule에 해당하는 이야기 이다. 모델이 어떻게 파라미터를 최적화 시키도록 할것인가? 지시하는 Rule이라고 할 수 있겠다.
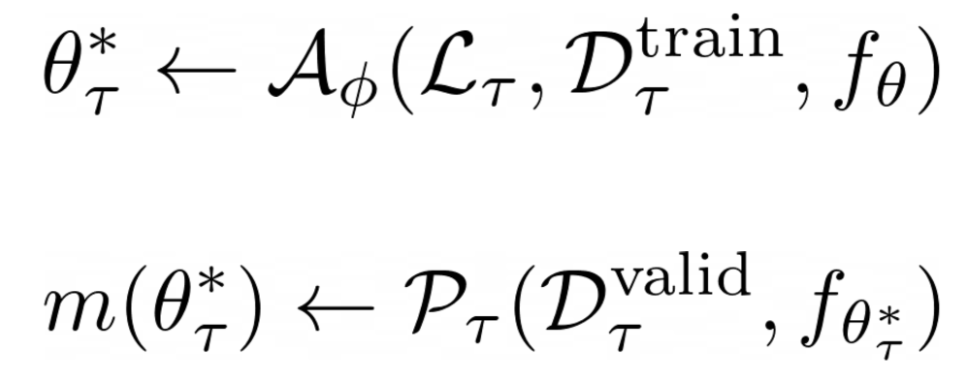
머신러닝의 가장 기본적인 모형인 선형회귀와 로지스틱회귀를 생각해보자.
선형회귀에서는 비용함수를 최소화 하는방법으로 기본적으로
(1)정규 방정식, (2)경사하강법을 사용하게 된다.
로지스틱회귀(LogisticRegression)의 경우 비용함수를 최소화 하는 방법으로
(1)경사하강법과 (2)-뉴튼 랩슨의 방법으로
scikit-learn기준, 이 두가지 방식을 베이스로 변형을 추가한 알고리즘을 사용하게 된다.
이러한 차이는 무엇일까?
우선,
선형회귀에서 정규 방정식을 사용할 수 있는 이유는 파라미터의 추정값이 Closed form solution으로 바로 해답을 찾을 수 있기 때문이다.
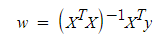
Closed form solution은 2차 방정식의 근의 공식과 같이 특정 함수 해를 특정 연산으로 바로 찾는 solution을 말한다.
그러나 데이터의 차원이 커지면 커질수록 데이터 포인트들의 요솟값들(데이터의 피쳐들)간의 다중공선성이 있는 경우 이러한 파라미터의 추정값은 정확하지 않게되고, 또한 Matrix의 크기가 커질수록 계산이 복잡해지는 단점이 있다.
그래서 선형회귀의 경우에도 위의 식과 같이 closed form soluton이 있지만
경사 하강법(graident descent)으로 최적의 파라미터를 추정하게 된다.
이러한 방법을 closed form solution을 대비하여, "Iteratvie method" 혹은 "numerical solution"등으로 표현한다.
대부분의 머신러닝 딥러닝의 Learning Rule로 gradient descent를 채택하기 때문에 무심코 지나칠 수 있는 부분이지만, 가장 처음에 배우는 가장 간단한 모형인 선형회귀로 부터 이러한 차이를 알고 가는 것은 의미가 있다.
그렇다면 LogisticRegression은 정규방정식이 아니라 어째서 경사하강법과 뉴턴랩슨의 방법을 사용하는걸까?
우선 LogisticRegression의 경우에는 Closed form solution이 존재하지 않는다. 즉, 정규방정식을 사용할 수 없다.
gradient descent와 같은 Iterative method, numerical solution으로 파라미터를 추정해나가야만 하는데, 그러한 또 다른 방법(learning rule)으로 Newton raphson method가 있는 것이다.
사이킷런이 제공하는 LogisticRegression()의 solver는 다음과 같은것을 확인할 수 있는데

solver란 비용함수를 최소화하는 알고리즘을 즉 Learning Rule을 말하고,
(2)liblinear, (5)sag, (6)saga는 경사하강법의 변형 방식이고,
(1)lbfgs, (3)newton-cg, (4)newton-cholesky는 뉴튼-랩슨 방법의 변형이다.
참고적으로 solver값을 별도로 설정하지 않았을때 default로는 (1)lbfgs를 사용하여 학습하게 된다.
sag는 (Stochastic Average Gradient descent)의 약어로 확률적 경사하강법(SGD)를 활용한 방법이다.
과거의 경사를 기억하여 최적화의 속도를 좀 더 높힌 방식이라고 한다.
saga는 sag의 방식에서, 다양한 규제화를 쓸 수 있도록 변형한 방식이라고 한다.
이 외의 자세한 내용은 사이킷런 공식 문서를 참고하도록 하자.

각 solver의 종류마다 사용 할 수 있는 규제화(regularization) 방식에는 차이가 있다.
일반적으로 solver와 규제화의 선택에 따른 모델의 예측성능이나 학습속도가 큰 차이를 보인다고 할 수 없지만,
특징적인 점은, 데이터셋의 크기가 적은편이라면 일반적으로 좋은 성능을 발휘하는'liblinear' 방식을,
더 큰 데이터셋이 주어졌을 경우 'sag'나 'saga'의 방식을 취하는 것이 성능이 좋은 편이라고 하니, 이쪽을 우선적으로 고려할 것 같다.
두 방법의 차이에 대해서 조금 더 자세히 알아보자.
1. 경사하강법 (gradient desecent)
$$b_{i,new} = b_{i,current}\,-\,\eta\frac{\partial E}{\partial b_i} ,(=b_i,current에서의 slope)$$
$\eta$ 에타 ;: 학습률(Learning Rate) , hyper-parameter로 직접 조정해줘야 하는 값이다.
크면 클수록 업데이트량이 많다.
그렇다면, 많이 업데이트 하는게 좋은건가? 업데이트는 언제까지 해줘야 하는걸까?
(1) 변화가 거의 없을때 까지 해줄수 있다.
$$|b^{n+1}-b^{n}|\leq \partial$$
또는
(2) 특정 횟수 만큼 반복할 수 있다.
(max_iter = n)
그렇다면, 많이 업데이트 하는게 좋은건가?
-> 업데이트를 많이하는것에는 장,단이 있다.
Learning Rate를 크게 할 경우: 최솟값으로의 수렴을 보장 할 수 없게 된다. (세번째 그림)
Learning Rate를 작게 할 경우: 연산량이 너무 많게 된다. 학습해야할 파라미터와 데이터 수가 많으면 큰 문제가 된다.
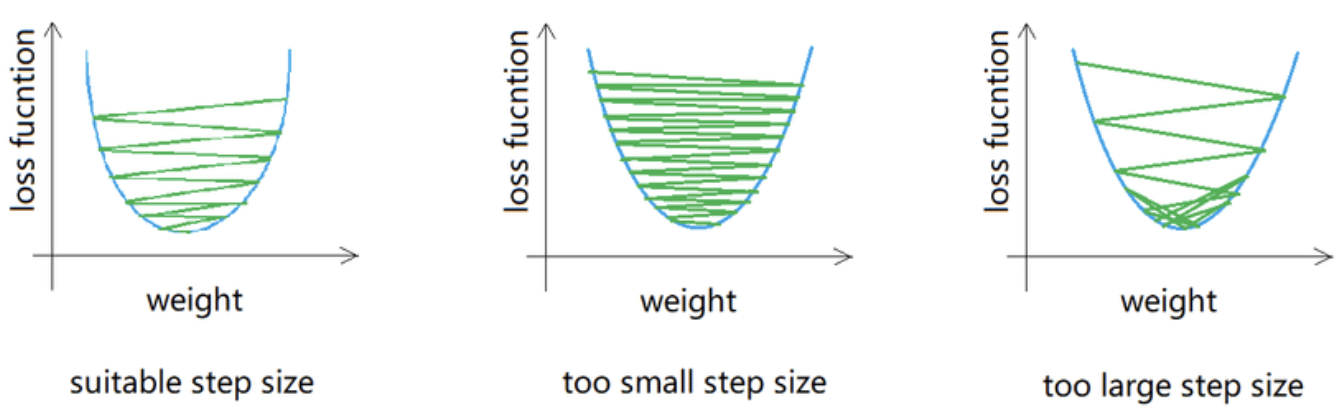
그렇다면 Learning Rate를 어떻게 설정하는게 좋은걸까?
경사하강법에서의 Learning Rate를 특히 Step size라고 하며, 이러한 Step size에 관해 살펴보는 것이 또 다른 주요 과제가 된다.
Step size는 모델마다 상황마다, 적당히 알려진 값이 있음으로 논문을 참고하는 방법이 좋다고 한다. thanks to giants!
2. 뉴튼-랩슨 방법 (Newton–Raphson method)
8. 2계 도함수법(뉴턴법 등)
1계 도함수법은 그래디언트를 이용해 목적함수의 1차 근사를 하는 최적화 방법이다. 이에 비해 2계 도함수법은 헤시안 등을 사용해 2차 근사를 이용한다. 1계 도함수법에 비해 많은 정보를 활용
velog.io
what is Newton–Raphson method?
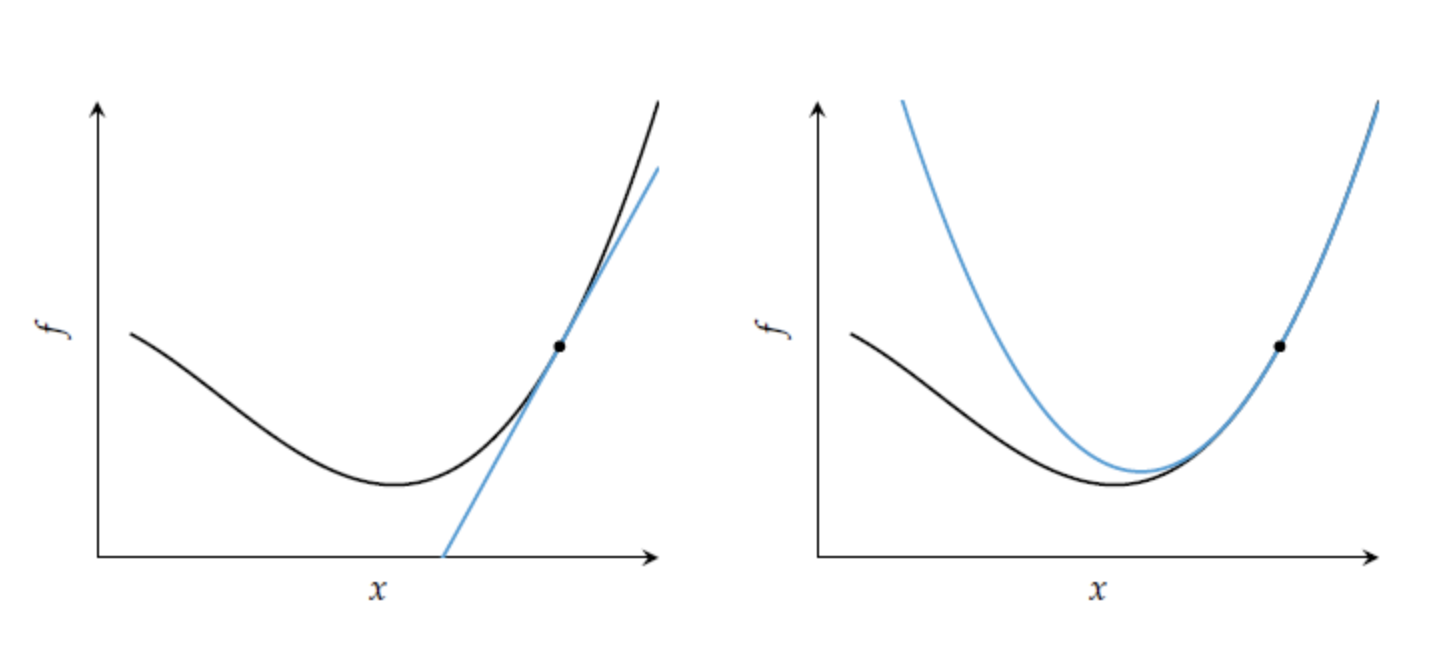
아래의 그림과 같은 비선형함수, $f(x)$가 주어져있다.
$f(x)=0$에 대한 해를 찾는 특정한 방법을 모른다면, 어떻게 해를 찾을 수 있을까?
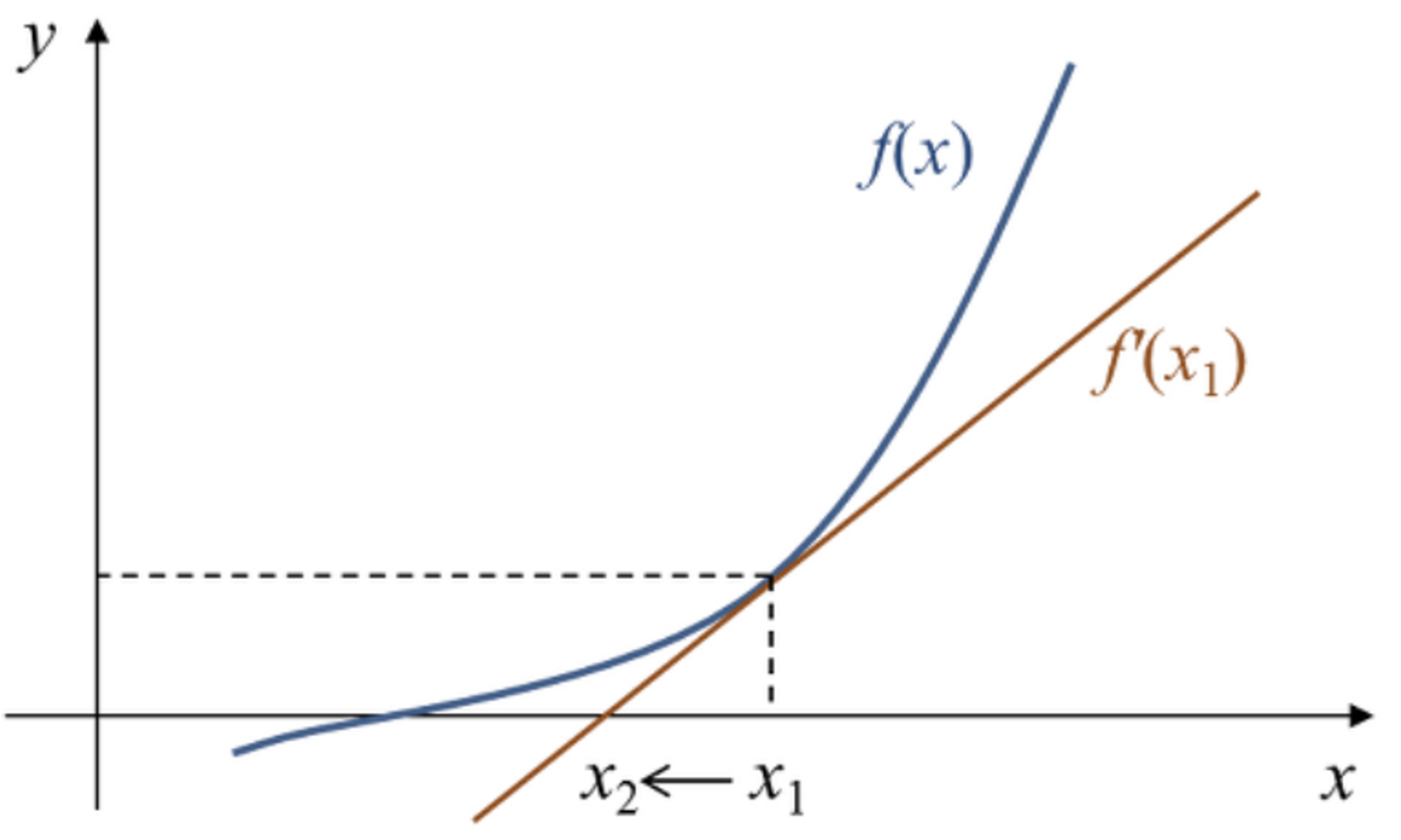
우선, $y = f'(x_n)(x-x_n)+f(x_n) , y=0$ 을 만족하는, $x_{(new),n+1}$ 을 찾자.
$x_{(new),n+1}$ 에 대해서 매번 새로운 접선을 그어가며
$|x_{new+1}-x_{new}|$ 가 매우 작은 값으로 수렴해 갈때, 뉴턴법을 종료하게 된다.
뉴턴-랩슨의 방법을 이용하여 비용함수를 최소화 해보자.
(뉴튼-랩슨 방법은 비용함수의 최소화 뿐만 아니라 다양한 상황에 쓰일 수 있는 좋은 아이디어가 된다고 한다.)
우선 뉴튼랩슨 방법을 이용하기 위해서, 아까의 비선형 함수 $f(x)$를 테일러 전개의 2차 근사를 해주면
경사하강법에서 발생했던 step size를 직접 설정해주어야하는 문제를 해결할 수 있다.
$$q(x)=f(x_k)+(x-x_k)f'(x_k)+\frac{1}{2}(x-x_k)^{2}f''(x_k)$$
참고글을 통해 살펴볼 수 있듯이, 뉴튼 랩슨의 방법에서 새로운 $x_{k+1}$을 을 살펴보면,
$$x_{k+1} = x_k - \frac{f'(x_k)}{f''(x_k)}$$
따라서 뉴튼 랩슨의 learning rate는 이계도함수의 역수로 주어져 있음을 알 수 있다.
그러나 결국 이를 사용하기 위해서는, 각 파라미터에 대해 1차 미분(그래디언트)과 2차 미분(헤세 행렬)을 모두 사용하여 업데이트를 해야 하는데 연산량이 경사하강법 대비 많아지고, computational cost가 더 들게 된다.
다시 정리하자면, 모든 파라미터에 대한 이계도 함수를 구하는것은 컴퓨터도 쉽지만은 않은가 보다.
뉴튼 랩슨의 방법보다 경사하강법을 이용한 방법이 연산상에 이득이 있음으로, 더욱 일반적이고,
현재까지의 대부분의 머신러닝과 딥러닝은 모두 gradient descent를 사용하고 있다고 해도 과언이 아니다.
모두 gradident descent의 변형들을 사용하고 있다. step size;:Learning rate만 적당히 잘 조정하면 된다.
'기초 노트 > MachineLearning' 카테고리의 다른 글
| Stacking과 Blending의 차이 설명 (3) | 2024.03.06 |
|---|---|
| 원-핫 인코딩의 모든 것(feat.OneHotEncoder vs pd.get_dummies) (1) | 2024.03.05 |
| 데이터의 차원이 뭔가요? (1) | 2024.02.21 |
| 편향(Bias)와 분산(Variance) 그리고 Bias-Variance Decomposition (1) | 2024.02.16 |
| Loss Function vs Cost Function vs Objective Function은 무슨 차이 인가요? (0) | 2023.07.01 |




