
이번 강은 Backprogation(역전파)에 대해서 다룬다.
지금까지의 내용은 Linear Classification의 한계를 넘어서는 NeuralNet의 특징, Space Warping과 Activation fucntion을 추가하여 비선형적인 표현을 할 수 있는 것, Universal Approximation에 대한 개념과 신경망의 Loss surface는 다양한 형태의 Non-convex function으로 존재함에도 불구하고 optimization되어 실전에서 어떻게든 작동한다고 배웠다.

또한 위와 같은 loss function으로 현재의 가중치에 대한 happiness or unhapiniess를 표현하고, SGD와 같은 알고리즘으로 가중치를 업데이트 한다고 배웠다.
여기서 문제는 gradient를 어떻게 계산할 것인가? 에 대한 것이었다.

gradient를 계산할 수 있는 가장 naive한 방법은 그냥 종이에다가 편미분식을 써보는 것이다.
편미분을 하게 되면 많은 항이 포함된 거대한 방정식이 나올 것이다.
만약 SVM loss나 Cross Entropy에 대한 미분식을 각 Weight Matrix에 대해서 수행한다면 종이가 엄청 필요할 것이다.
또한 간단한 Linear model에 대해서는 종이에다가 gradient 수식을 적을수야 있겠지만 더 복잡한 형태의 모델로 확장하기 쉽지가 않다. NueralNet의 아키텍쳐가 바뀔때마다, 예를 들어서 레이어 2개짜리에서 5개짜리로, Cross Entropy Loss에서 SVM loss로 바뀔때마다 매 가중치마다 편미분해야되며 이를 모두 다 수식으로 옮겨 적어줘야만 할 것이다.
따라서 다양한 아키텍쳐와 loss function에 확장가능하기 위해서, gradient를 구할때 모듈화된 접근이 필요하다.
물론 데이터사이언티스트 혹은 연구자로서 gradient를 직접 구할 일은 없다.

gradient를 구하는 일은 computational grapgh라고 불린다. computational grapgh는 모델의 연산과정을 표현한 그래프이다. 왼쪽에는 우리의 데이터 $X$와 learnable parameter인 $W$가 주어진다. 바로 오른쪽 노드에는 어떠한 연산뭉치가 주어진다. 파란색의 노드는 input $X$와 weight matrxi $W$간의 어떠한 matrix multiplication를 의미하고, 빨간색의 노드는 SVM Classifier를 위한 hinge loss를, 초록색의 노드는 모델의 regularization term을 의미한다. computational graph의 output은 scalar값인 loss $L$이다.
간단한 모델에 대해서 이러한 computational graph를 기술하는 것은 다소 어리석게 보이거나 귀찮게 보일수도 있다. 그러나 더 복잡한 모델로 갈수록 computational graph를 기술하는 것은 매우 중요하게 된다.

AlexNet의 구조를 예를 들어보면 가장 윗단의 input으로는 image가 들어가고, 7개의 Convolutional layer가, 가장 아랫단에는 regularization을 포함한 scalar loss가 나오게 된다.
이 구조 전부의 gradient를 계산하라고 하면 손사레 칠 것이다. 우리는 computational graph를 만들고 모델이 수행하는 모든 연산의 결과의 data structure를 추적하고, 표현하고자 할 것이다.

computation 수업에서 등장하는 Neural Turing Machine의 예시이다. 아마도 수업의 첫부분에서 인공신경망이 튜링머신의 soft differentiable approximiation이라고 배울 것이다. 위의 그림이 미분가능한 튜링머신의 computational graph의 모습이다. 매우 복잡하고 이 것을 직접 gradient계산하는 것은 끔찍한 일이다. 더 끔찍한 것은 사실은 이것은 단 한번의 iteration이여서

실제로 풀어보면 마치 RNN처럼 매우 복잡한 형태일 것이고 모듈화된 gradient를 구할 수 있는 방법인 computational grapgh의 필요성을 더욱 느끼게 된다. 이제 computational graph의 필요성을 알았으니 구체적으로 gradient를 어떻게 구하는지에 대해 간단한 모델을 통해 알아보자.

위의 예시에서는 세가지 scalar variable $x,y,z$가 있고 output은 $(x+y)z$고 이를 통해 loss를 계산한다고 생각해보자.
'backpropatation'은 위와 같은 computational grpah에서 gradient를 구하는 방법이다.

먼저 $x =-2$, $y=5$, $z=-4$라고 생각해보자.
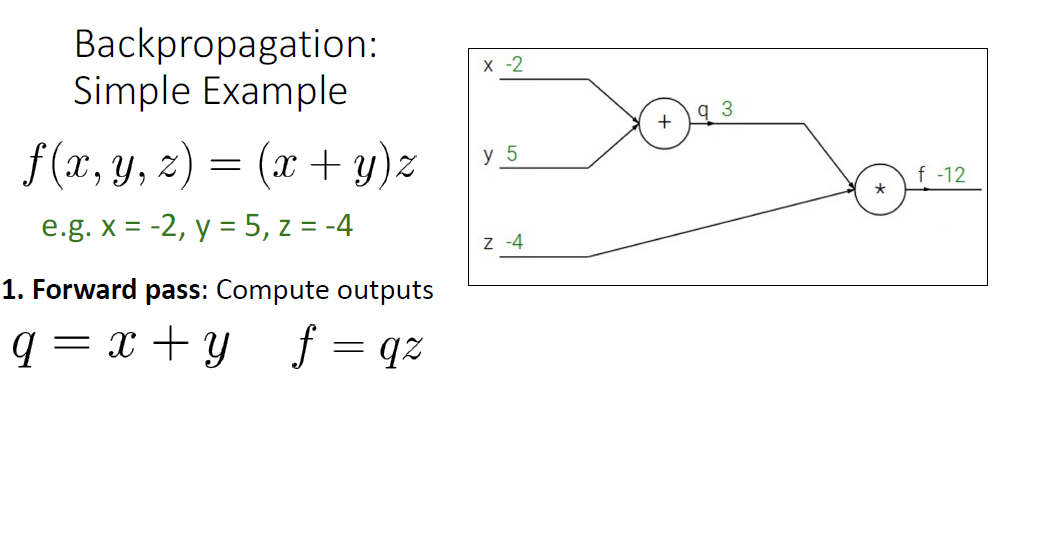
computational graph를 이용하는 첫번째 스텝은 바로 'Forward pass(순전파)'이다.
Forward pass에서는 ouput value를 구하기 위해서 왼쪽에서 오른쪽으로, input value로 부터 node에 적혀진 연산을 수행하는 것을 말한다.
여기서 우리는 $x+y$의 연산 결과를 통해 중간 변수인 $q$를 얻고 $*z$연산을 통해 ouput value인 $f$를 얻는다.

이제 ouput $f$를 각각 input value에 대한 미분값 $\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}$을 구해야 한다. 이것은 Forward pass와 반대 방향으로 진행되며 Backward pass라고 부르고 우리가 Backpropataion이라고 부르는 이유이다.

첫단계는 \frac{\partial f}{\partial f}를 구하는 것이다. 매우 간단하다. 1이다.

backpropataion을 위한 계산을 할때, 다이어그램에는 value값은 위에 gradient에 대응되는 값은 아래에 적는식으로 계산한다.
두번째로 $\frac{\partial f}{\partial z}$를 계산하려면 $f=qz$라는 중간 연산에 대해 살펴봐야 되는데

$\frac{\partial f}{\partial z} =q$와 같다. 원래 q값의 value가 3이었기 때문에 $ \frac{\partial f}{\partial f}$의 값은 3이 된다.

다음 계산은 $\frac{\partial f}{\partial q}$인데, 동일하게 local derivative인 $\frac{\partial f}{\partial q}=z$ 인 것을 알고
z값의 value가 -4이기 때문에 $\frac{\partial f}{\partial q}=-4$ 이다

여기서 우리는 Chain Rule이 필요한다. input $y$를 보면 ouput $f$와 직접적으로 연결되어 있지 않은 모습이다.
$\frac{\partial f}{\partial y}$를 구하기 위해서는 $y$가 중간 변수인 $q$에 대해 미치는 영향력을 알아야 한다.
일변수 미적분학에 등장하는 chain rule을 통해 우리는 $\frac{\partial f}{\partial y}= \frac{\partial q}{\partial y} \frac{\partial f}{\partial q} $ 임을 알고, $y$가 조금 변하면 $q$가 조금 변하고, $q$가 조금 변함에 따라 $f$가 조금 변하는 것을 안다.
$f$가 $y$에 따라서 변화하는 양은 두 효과를 곱함으로써 설명할 수 있게 된다.

인공신경망의 컨텍스트에서는 이러한 세 요소에 각각 특별한 이름을 붙인다.
"Downstream Gradient", "Local Gradient", "Upstream Gradient"
"Downstream Gradient"는 현재의 step에서 우리가 구하고자하는 미분계수이다.
"Local Gradient"란 이름은 현재의 $y$값이 다음 스텝의 intermediate 변수인 $q$에 얼마나 영향을 미치는지에 대한 Local적인 정보이기 때문에 붙었다.
"Upstream Gradient"란 이름은 우리가 현재 $y$라는 변수에 대해서 관찰하는 상황에서 Downstream gradient가 final ouput에 대해 얼마나 영향을 주는지를 나타내는 부분으로, ouput($q$)이 final ouput에 얼마나 영향을 주는지 나타내는 부분이다.
우리는 Chain Rule을 활용하여 Local Gradient와 Upstream를 곱함으로써 간단히 Downstream Gradient를 구할 수 있고 이 과정은 반복된다.
이러한 gradient를 구하는 방법은 모듈화될 수 있기 때문에 매우 유용한 방법이다.

Computational Grapgh의 노드 한단위를 자세히 살펴보자. 이 장면에서 Gradient를 구할때는 다른 노드의 부분이나 이전레이어나 앞선 레이어의 어떠한 graph정보도 필요하지 않다. 단지 "Local Processing"을 할 뿐이며, Global computing은 단순히 Local Processing을 전체 그래프를 순회하면서 계산함으로써 이뤄진다.
위의 세팅에서는 local function $f$는 input $x$와 $y$를 받는다. Forward pass 동안에는 Local ouput $z$를 만들어낸다. 만들어진 $z$는 다른 노드에서 활용될텐데, 그 활용을 현재 단계의 노드에서는 전혀 상관하지 않고 단순히 전달(forward-pass)할 뿐이다.

이러한 계산은 위의 사진처럼 Local한 모듈 내에서 모델의 Global structure에 대한 어떠한 고려도 없이 단순히
Local Gradients를 계산하고, final ouput으로 부터 전파되어온 Upstream gradient와 곱하기만 하면 Downstream gradients를 얻고, 이 때 이 Downstream gradients가 다른 노드에서 어떻게 쓰이는지는 전혀 상관하지 않은 체로 local한 범위에서만 계산하여도 단순히 전파만 한다면 Network의 모든 gradient가 계산 된다.
이것은 머리를 싸매며 종이에 방대한 미분을 때리고 있을 시간에 단순히 모듈 하나만 계산하면 되니 실로 놀라운 발전이다.

Computational Grapgh에 대한 다른 예를 들어본다. Logistic Classifier에 대한 예시가 되겠다.
좌측에는 총 5개의 변수, $w_0,x_0, w_1_x_2, w_2$가 있다.
forward-pass에서는 $w_0, w_1$과 $x_0,x_1$를 각각 내적하고 bias term인 $w_2$를 더할 것이다.
이후에는 $f(x,w)$에 보이는 것처럼 $e^-$를 취하고 1을 더한뒤에 역수를 취한다.

forward-pass 단계에서는 앞선 예시처럼 forward function을 이용하여 각 노드의 값을 계산한다. 결과는 모두 scalar이다.

Backward-pass에서는 final scalar output으로 부터 Local gradient를 계산하고, 이게 첫 Upstream gradient가 되어 각각의 노드마다의 Downstream gradient를 구할 것이다.
첫번째의 미분값은 자기 자신을 미분하기 때문에 항상 1로 출발한다.

upstream gradient '1'을 획득한 상태에서, $frac{1}{x}$의 Local gradient는 $-frac{1}{x^2}$임을 알고 있기 때문에 $x$값으로 1.37을 대입하고 upstream gradient 1을 곱하여 -0.53이 나오는 것을 알 수 있고

마찬가지로 $x+1$의 local gradient는 1이고 upstream gradient는 -0.53이었기 떄문에 곱하면 Downstream Gradient는 동일하게 -0.53이다.

$e^x$의 미분은 아시는 바처럼 자기 자신 그대로이고, upstream gradient -0.53에 $e^x$에 -1을 대입한 값인 0.36 (local gradient) 을 곱하면

$-0.53 \times e^-1 = -0.20$(downstream gradient) 이 나오게 된다.

역시 동일하게 계산하고,

계속 Backward Backward Backward하면 된다.
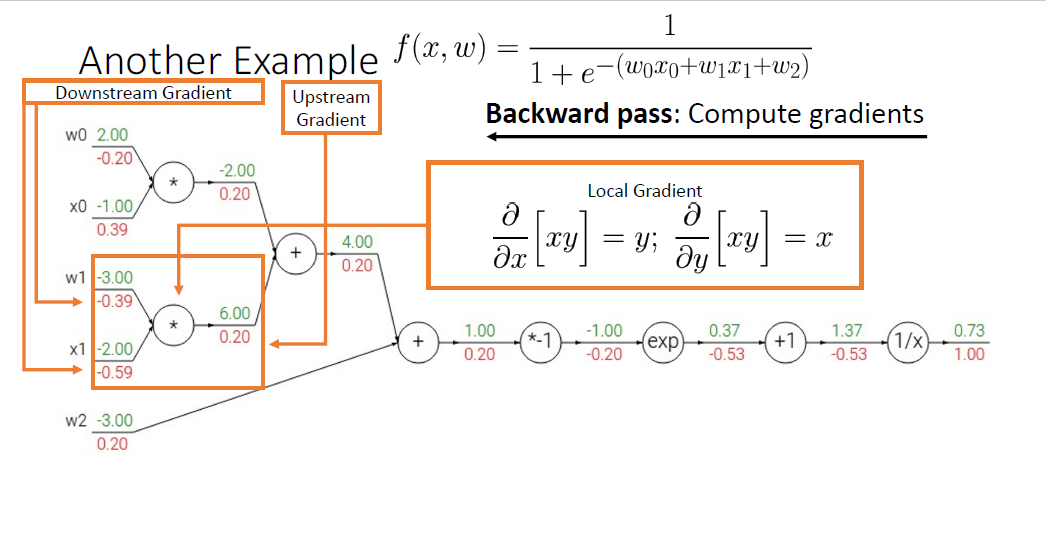
물론 지금과 같이 하나 하나씩 Baisc module을 계산하는 방법도 있겠지만
여기서 흥미로운 점은, 특정한 Computational Grapgh에서는 어떠한 연산 구조에 대해 여러가지 생각을 해볼 수 있는 점이 있다는 것인데,

어떤 노드들에 대해서는 노드 뭉텅이로 한번에 독립적으로 연산을 할 수도 있다.
파란색 박스친 sigmoid라는 함수는 사실 (사실 머신러닝 컨텍스트에서 너무도 많이 쓰이는) backpropagation 과정에서 쉽게 계산될 수 있다.

시그모이드 함수를 미분하면 다음과 같이 단순히 (시그모이드의 출력값)과 (1-시그모이드 출력값)을 곱한 형태로, 매우 간단한 형태를 띄는 것을 알 수 있다.
이것이 의미하는 바는, 중간 과정의 노드에 관한 정보를 저장할 필요 없이, 파란색 박스친 영역의 부분에 대해서 Local Gradient를 매우 쉽게 계산할 수 있다는 뜻이다.
따라서 그래프 디자이너는 이렇게 쉽게 계산가능한 형태에 대해서는 backwardpass를 더욱 효율적으로 디자인 할 수 있다.

그래서 파란색 청크의 좌우의 input과 output을 통해서 Backward pass를 수행할 수 있으며, 중간단계 노드의 계산 과정은 모두 생략해도 상관없게 된다. 이러한 방법은 계산 과정에서도 더욱 효과적이고, 함수의 의미적인 부분도 살리기 때문에 Computational Grapgh계산과정에서 일반적으로 쓰이는 방식이다.
local gradient를 계산할 때 $x$가 아닌 시그모이드 함수의 출력값인 $\sigma(x)$에 대한 정보를 대입해야 함을 주의하자.

사실, Computatioanl Grapgh에서 맞이하는 각 노드의 연산에는 어떠한 Backpropagation Pattern이 존재하는데
먼저, add gate의 경우 backward pass동안 gradient distributor로 작동한다. forward pass의 경우에는 output값은 input값을 더한 형태이지만, backward pass의 경우에는 local gradient가 1이기 때문에 upstream gradient가 downstream gradient에 그대로 전파된다.
두번째로 copy gate의 경우, gradient adder의 형태로 작동한다. forward pass의 경우에는 값이 양쪽으로 복사되어 전파되지만, backward pass의 경우에는 각각 동일한 영향력인 gradient가 더하여 전파된다. 이런 연산을 왜하냐? 싶을 수도 있겠지만 예를 들어 regularization term을 추가해야 할때, weight에 대한 동일한 정보를 흘려야 되기 때문에 이러한 연산을 수행한다. 모델의 메인 branch에서는 weight matrix를 통해 score를 계산하고, 서브 branch에서는 L1이나 L2와 같은 regularization term을 계산하는 것이다. 그리고 동일한 weight를 가지고 서로 다른 task를 진행해야 할 때, weight의 정보를 복사하기 위해서 이러한 branch를 사용한다. 다시 한번 중요한 점은, forward pass 동안에는 동일한 weight값을 이용하기 위해 동일한 값을 복사하고 이를 각 branch에 전파 하였지만 이들은 서로 다른 목적으로 사용되었기 때문에, backward pass동안에는 서로 다른 gradient값이 전파된다는 것이다. 흥미로운 점은 copy gate와 add gate가 서로 반대작용을 한다는 것이다.

세번째 특징적인 게이트는 multiplication gate이다. 예를 들면 $z=xy$와 같은 형태가 있겠다. Downstream Gradient를 계산할때 Upstream Gradient와 다른 input값이 곱해지는 형태를 취하게 된다. multiplication gate는 forward pass에서도 곱셈 연산을 하지만 backward pass에서도 어쨋든 다른 값을 곱하는 형태를 취한다. 이것은 때때로 매우 긴 형태의 곱셈이 되어 특정 모델에는 큰 문제를 발생시키도 한다. (아마도 곱셈을 하려면 메모리에 계속 gradient를 저장해야되는 이슈를 말하는 듯)
마지막으로 자주 볼 수 있는 게이트는 max gate인데 이것은 마치 ReLU function처럼 작동해서, max값의 노드쪽으로는 upstream gradient를 그대로 전파하지만, 그 외의 값에는 모두 zero gradient를 흘리게 된다. 이것은 gradient router라고도 불린다. 모델에 이러한 max gate가 많게 되면 zero gradeint를 자주 흘리게 되고, gradient flow에 문제가 발생하게 된다. 이러한 이유로 max gate를 사용하는 것은 자주 권장되지는 않는다.
사실 이러한 간단한 수학적 연산이 대단하지 않아 보일 수 있는데, 이러한 간단한 구조가 매우 커다란 신경망을 통해서 gradient가 flow되고 결코 간단치만은 않은 결과를 만들어 낸다는 것이 흥미로운 것이다.

이제는 수식으로 전개하는 것 보다 코드로 어떻게 이것을 적용하는지 살피는 것이 더 도움이 될 것 같다.
보이는 간단한 함수는 single batch 데이터를 받아서 loss를 계산하는 linear classifier가 되겠다.
보통 Backpropatation의 implementation으로는 크게 두가지가 있는데 하나는 "Flat"한 버전이라고 불리는 코드이다.

"Flat"버전의 Backpropagation코드에서는
Forward pass단계는 output을 계산하고, Backward pass는 Forward pass의 반대 방향으로 gradient를 계산하는 코드를 그대로 이어 적으면 된다.

Backpropagation에서 가장 첫단계로, Base case는 gradient가 1이었고,
앞선 시그모이드의 chunk의 예시처럼, 시그모이드를 미분하면 $(1-L)\times L$의 꼴이고,

add 게이트는 gradient distributor의 역할을 수행하며


Mul 게이트는 swap multiplier의 역할을 수행하는 모습을 볼 수 있다.

gradient code를 적을때 어떠한 수학도 사용되지 않았다. 단순히 배운 local rule대로 forward pass를 적고 backward pass를 적고 끝이다.

2번과제가 SVM Loss에 대하여 flat버전의 backpropagation 코드를 적는 일이 될 것이다.

현장에서 더 많이 사용되는 Backpropagation의 implementation 방법은 Modular API 방식이다.
위의 예시는 실제 코드는 아니고 pseudo code지만 대략 노드의 연산에 대한 객체를 정의하고, 노드들을 topoligically 정렬한 뒤 계산하게 된다.

파이토치에서는 torch.autograd.Function을 상속함으로써 간단한 computatioanl grapgh의 연산에 대한 객체를 만들 수 있다.
forward 함수는 input $x$와 $y$를 받고, 여기서 $x$와 $y$는 아마도 torch.tensor이 형태일 것이며, $ctx$는 backwardpass의 gradient의 계산 및 저장을 위한 state를 보관하기 위한 context object라고 한다.
backward 함수에서는 동일한 context object인 $ctx$를 받고, 이로부터 우리는 bacwkardpass에서 필요한 forward pass의 정보를 context object 객체에서부터 뽑아낼 수 있다.
위의 코드는 두 개의 스칼라 값을 갖는 torch.tensor에 대한 실제 파이토치 코드이다. 그래서 이것을 따로 활용하는 것을 추천하지는 않지만,
파이토치를 사용하는 중에 어떤 독립적인 기능을 구현해야 한다고 하면 이런식으로 적어야되는 것을 알려준다.

그래서 파이토치가 뭐냐? 파이토치는 어떻게 보면 작은 함수들에 대해 forward와 backward가 기술된 Autograd Engine이다.

파이토치 레포에서 한 파일을의 장면을 뜯어서 살펴보면,

sigmoid의 forwardpass 부분을 살펴볼 수 있고 (C++이나 C에 의존성이 있는 부분이다.)

이것을 사용하지 않으면 스파게티 코드를 볼 수 있을 것이다.

두번째 페어의 함수는 backwardpass를 계산하는 THNN_Sigmoid_updateGradInput이란 함수이다.
C의 의존성이 있는 부분을 차치하고, 아무튼 계산하는 Backward부분을 보면 우리가 봐온 익숙한 부분을 그대로 사용한다.

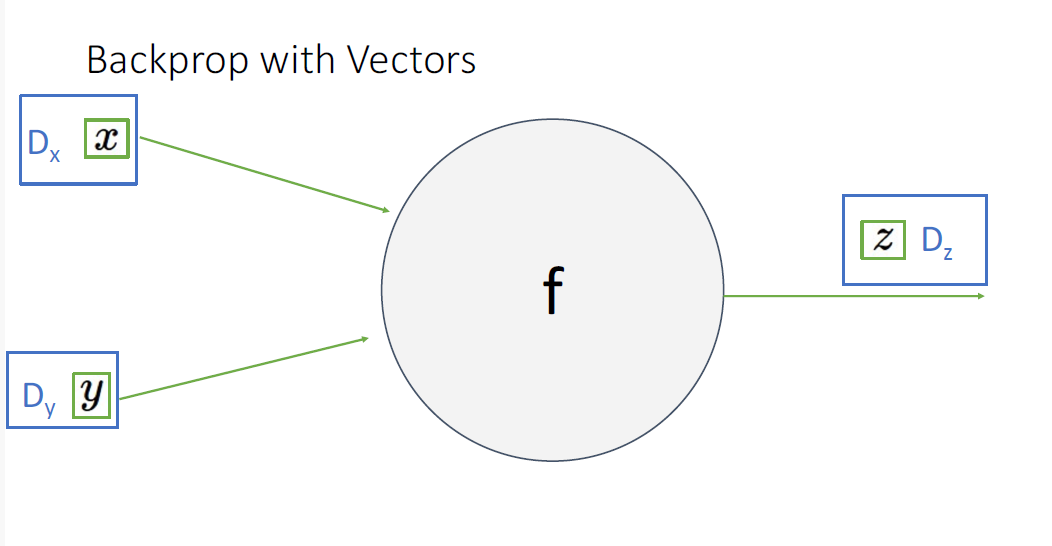
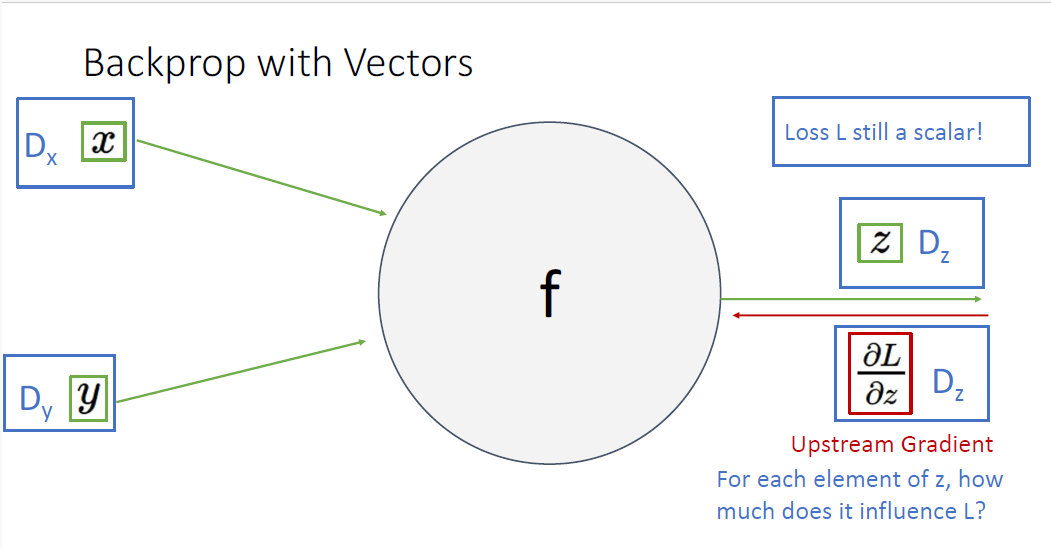
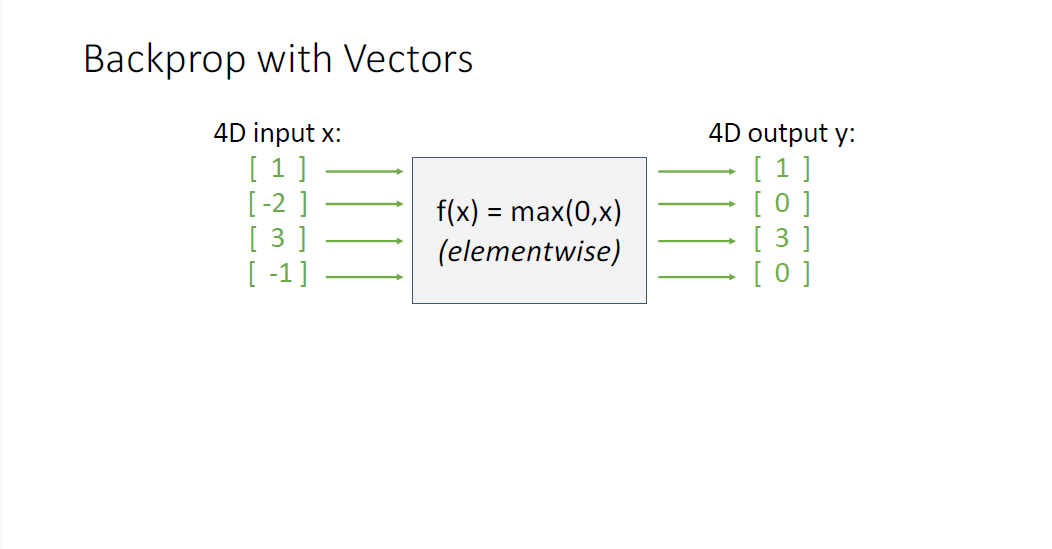
지금까지는 모두 scalar에 대해서만 다뤘지만 실제로 우리는 벡터를 다루는데, 벡터함수에 대해서는 어떻게 적용될까?

다변수함수의 미분에 대해서 다시 살펴보자. (작성중)














































'기초 노트 > EECS 498-007 (ComputerVision)' 카테고리의 다른 글
| EECS 498-007 Lecture 8: CNN Architectures 정리 (0) | 2024.04.02 |
|---|---|
| EECS 498-007 Lecture 07 : Convolutional Networks 정리 (1) | 2024.03.25 |
| EECS 498-007 Lecture 05 : Neural Networks 정리 (0) | 2024.03.17 |
| EECS 498-007 Lecture 04 : Optimization 정리 (0) | 2024.03.15 |
| EECS 498-007 Lecture3 : Linear Classifiers 정리 (0) | 2024.03.04 |