플로라도의 data workout
EECS 498-007 Lecture 07 : Convolutional Networks 정리 본문
EECS 498-007 Lecture 07 : Convolutional Networks 정리
플로라도 2024. 3. 25. 03:00

오늘 강의의 주제는 이미지 처리 분야의 가장 메이저한 모델인 Convolutional Networks이다.

지난 강에서는 Backpropagation 알고리즘에 대해 배웠다. 복잡한 네트워크 구조의 gradient를 전부 계산하는 것이 아니라
저장된 forward pass의 정보를 이용하여 local한 연산을 통해 gradient를 계산하는 방식이다.
또한 이러한 방식을 활용하는 방법 중, Modular API방식으로 활용하는 것을 배웠다.

다음으로는 Linear Classifier과 신경망의 Fully connected Linear Classifier에 대해서 배웠다. 많은 함수를 표현할 수 있는 강력한 성질이 있지만, 두 모델의 구조 모두 2D의 공간적 구조를 고려하지 못하고 input RGB이미지를 flatten 시킨 거대한 column vector의 형태로 다룸으로써, 공간적 정보가 파괴되는 문제가 있었다.

머신러닝 모델을 우리가 빌드할때는 데이터의 구조를 고려한 모델의 설계가 중요한데, 따라서 이러한 2D 이미지의 특성을 고려할 수 있는 새로운 computational graph와 backpropagation 알고리즘을, 다시 말해 이미지에 대한 새로운 연산을 정의하면 될 것 같다. 이것이 바로 오늘 다룰 주제이다.
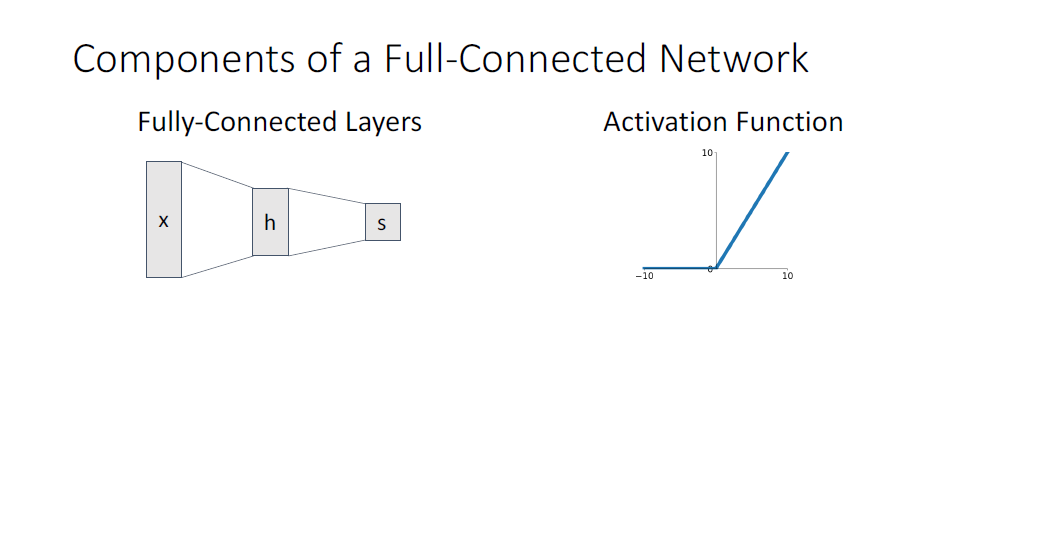
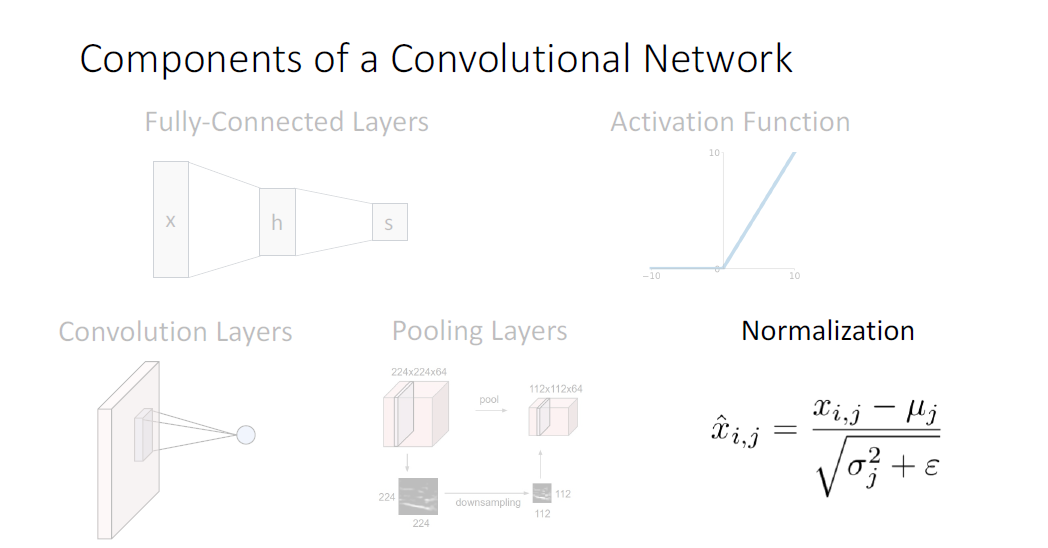
지금까지 살펴본 Fully Connected Network의 주요한 두 구성요소는 그 이름의 모태가된 Fully-Connected Layers와 Activation Function이었다.

Convolutioanl Networsk에서는 여기서 Convolution Layer, Pooling Layer, Normalization 세가지 요소가 추가된다.

첫번째로 볼 Convolution Layer는 Linear Layer과 동일하게 learable weight가 존재하나 spatial structure를 고려한다.

Fully-Connecte Layer를 다시 상기해보면, Forward pass동안 거대한 flattend vector로부터 (위의 예시는 아마 CIFAR-10과 같은 32*32*3의 RGB이미지) weight matrix와의 연산을 통해 output vector를 만들어 낸다.
Convoluton Layer도 마찬가지, input을 통해 동일한 형태의 output vector를 만들어낸다.

그러나 Convolution Layer에서는 더이상 flattend vector를 사용하지 않는다. RGB라는 3개의 채널의 볼륨을 가진 3차원 tensor를 사용하게 된다.

Convolutional Layer에서는 input tensor가 3차원의 구조를 가진 것 처럼, weight matrix도 동일한 3차원의 구조를 갖게 된다. 특별히 weight matrix를 Convolutional Layer를 다룰때 특별히 "filter"라는 용어를 사용하며, 우리는 필터를 통해 이미지를 슬라이드하면서 동일한 3차원의 output을 만들게 된다.

여기서 특징적인 점 한가지는, input tensor의 depth/channel은 필터의 depth와 대응된다.
다시 말해, 필터는 항상 input tensor의 full-depth를 고려한다. 물론 이러한 특징을 완화한 버전도 다음시간에 다룰 것이다.

3x5x5 filter를 사용하게되면 75개와 bias를 포함한 76개의 weight를 다루게 된다.
Linear Layer에서는 input x의 column과 weight matrix의 row간의 inner product연산이었다면,
Convolutional Layer에서는 input tensor의 local spatial chunk와 filter간의 inner product 연산이다.
대부분의 시각자료에서는 bias가 생략되어 있지만 일반적인 머신러닝 모델의 컨텍스트에서는 bias가 항상 포함된다는 것을 기억하자.

필터는 input tensor를 슬라이드하여 local chunk와 filter간의 inner product를 통해서 해당 영역이 얼마나 일치하는지에 대한 결과를 scalar로 만든다. 위의 예시에서 3x32x32 image를 3x5x5 필터로 전체 청크를 슬라이드하게 되면 1x28x28의 결과가 나오는데 이를 'activation map'이라고 한다.

서로 다른 convolutional 필터는 서로 다른 weight 값을 가지고 있으며 각각은 모든 local chunk를 순회하면서 output인 각각의 activation map을 만든다. 동일한 연산의 결과이지만, 사진의 파란색 activation map과 초록색 activation map은 서로 다른 값을 가질 것이다.

필터가 6개가 되면 필터의 shape은 앞에 6개가 추가된 형태인, 6*3*5*5의 shape을 갖는다고 할 수 있고,
마찬가지로 output인 activation map은 총 6개가 되어 6*28*28의 shape을 만들게 된다.

여기에 bias term은 필터당 1개 즉 6개가 더해지게 된다.

만약 input image가 한개가 아니라 배치단위로 다루게 되면 , input의 shape은 배치의 크기 $N$이 더해진 $N \timesC_{in} \times H \times W $의 4차원 Tensor를 다루게 되고 output은 마찬가지로 배치가 더해진 $N \times C_{out} \times H` \times W`$ 이 될 것이다.
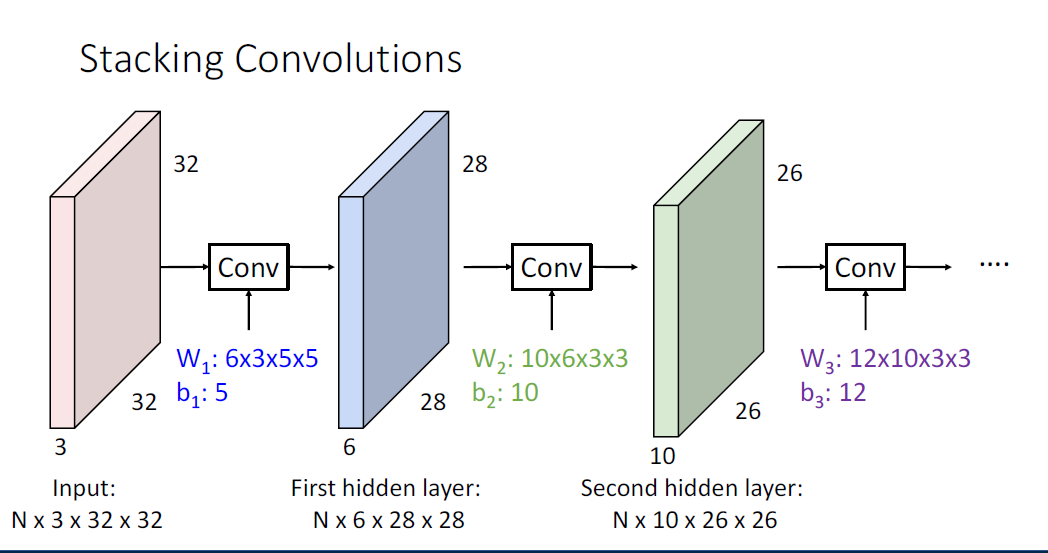
Convolutional Networrks는 Fully Connected Layer가 아닌 지금까지 봐온 Convolution layer를 쌓은 구조로 이뤄지게 된다.
Input으로 부터 각 필터의 사이즈와, hidden layer의 shape은 위와 같이 바뀌게 된다. (b1=6으로 정정,오타)

Convolution layer를 쌓을 떄 한가지 주의할 점이 있다.

Convolution layer도 앞서 살펴봤던 Linear Layer처럼 단순히 두개의 Convolution layer를 stack한 것은 한번의 Convolution의 연산과 동일한 효과를 얻게 된다. (어떠한 표현력의 추가도 하지 않는다.)

또 필터에 역할에 대해서 한번 살펴보자. 필터는 convolution layer가 갖는 가중치를 의미하는데,
필터는 과연 무엇을 학습하는 것인가?

Linear Classifier에서 각 가중치는 클래스별 한 벌의 템플릿을 학습하였고,

MLP에서의 가중치들은 전체 이미지를 포괄하는 템플릿을 학습하였다.

이에 비해 AlexNet의 예시를 살펴보면, 첫번째 conv layer를 통과한 필터는 어떤 local한 이미지 템플릿을 학습한 결과를 보여준다. 예를 들면 엣지의 방향이나, 색깔에 관한 정보같은 것들이다.

이번에는 지금까지 conv layer를 통과한 후 바뀌는 spatial dimension에 대해서 좀 더 자세히 살펴보자.

Input Tensor가 7x7의 그리드 형태로 주어지고 Filter 사이즈가 3x3이고 stride가 1이라면, 아래 슬라이드처럼 Intput tensor를 순회하면서 연산을 진행할 것이다.





convolution layer의 문제로는 레이어를 통과할 때 마다, output인 feature map의 spatial 사이즈가 input tensor보다 더 줄어든다는 점이다.

그래서 이를 해결하기 위해서 가장자리에 임의의 픽셀 값을 채워 넣는 "Padding"이라는 방법을 사용하는데, 주로 주변 픽셀의 평균으로 채워 넣거나, 근처의 값을 복사하거나 하는 방법도 있지만 대부분의 경우에는 단순히 '0'의 값을 채워 넣는 'Zero Padding'이란 것을 많이 사용한다.

일반적으로 얼마만큼의 영역을 패딩할 것인가는 Hyper-parameter $P$에 따라 결정되며 보통 input과 output의 사이즈가 같도록 설정하는 'Same Padding'방법인 (K-1)/2로 설정한다. 여기서 K는 필터의 사이즈이다.

convolution layer에서는 'Receptive Fields'라는 개념이 있다.
convolution layer의 연산은 필터가 어떠한 국소적인 영역을 관찰하는 것인데, 다시 말해 Output의 한 원소값은 필터가 바라보는 이러한 국소적인 영역에 의해서 영향을 받는다. 이 때 영향을 주는 국소 영역을 'Receptive Fields'라고부른다.

연속적인 Convolution layer의 형태에서는 위의 슬라이드에서 보듯이 Receptive fields사이즈가 K-1만큼 계속 커지게 된다.
여기서 조심해야할 부분은 Receptive field라는 단어가 모델의 Input에서부터 영향 받는 부분을 말하거나 또는 이전 레이어에어 의해 영향받는 부분만을 말한다는 점이다. 이것은 맥락에 따라 결정된다.

여기서 Receptive Fields 개념으로 관찰할 수 있는 것은, 우리의 Ouput의 한 원소가 Input Image 전체를 보기 위해서는 수 많은 레이어가 필요하다는 점이다.

따라서 우리는 Network에 Downsample하는 방법을 추가적으로 사용하게 되는데, 그러한 방법중 하나가 'Stride'를 부여하는 것이다.

Stride라는 것은 필터가 이미지 전체를 순회하면서 얼만큼의 간격을 두고 슬라이드할지를 나타내는 것으로, 아래의 슬라이드를 살펴보면 이전의 방식과 달라진 것을 알 수 있다. (이전 슬라이드는 stride=1의 경우이다.)
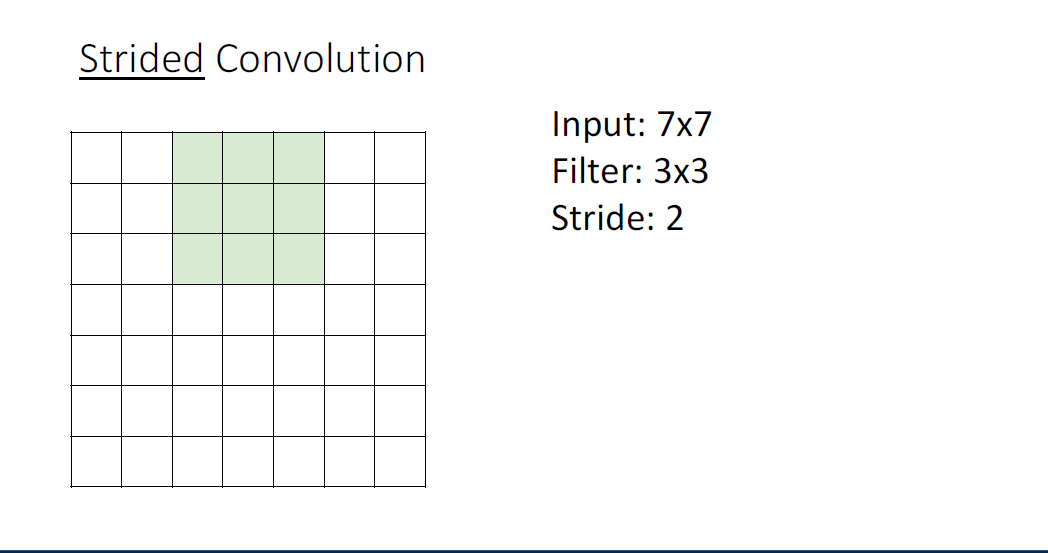


Stride를 사용했을 시, Output의 사이즈는 Stride크기 만큼의 비율로 줄어드는 것을 알 수 있다.

지금까지 배운 개념들로 hyper-parameter 세팅에 따라 shape을 확인해보자.






또 때때로 사용하는 것 중에는 1x1 Convolution이라는 것이 있다. 조금 의아하게 느껴질 수도 있겠지만,
1x1 Conv는 종종 매우 유용하게 사용된다. 각 커널은 1x1의 spatial size를 가지는데,
만약 input tensor를 feature vector의 그리드 형태로 생각해 본다면, 1x1 CONV는 Linear Layer에서처럼 각 피처마다 독립적인 연산을 수행한다고 볼 수 있다. (단 volumne을 가진 3차원의 그리드 형태이다.)

떄떄로 어떤 네트워크 구조를 보면
[1x1 Conv - ReLU - 1x1 Conv - ReLU ...]
와 같이 1x1 Conv와 ReLU가 시퀀스형태로 쌓은 것을 볼 수 있는데,
이것은 Network in Network라고 부르며 Fully connected layer의 연산 효율적인 버전이라고 생각할 수 있다.

지금까지 Convolution에 대해 배운 것을 요약하였다.

지금까지는 2D Convolution을 다루었는데, 2D Convolution이란 3차원의 텐서를 input으로 받고, 필터가 움직이는 영역이 2D의 공간임을 말한다.
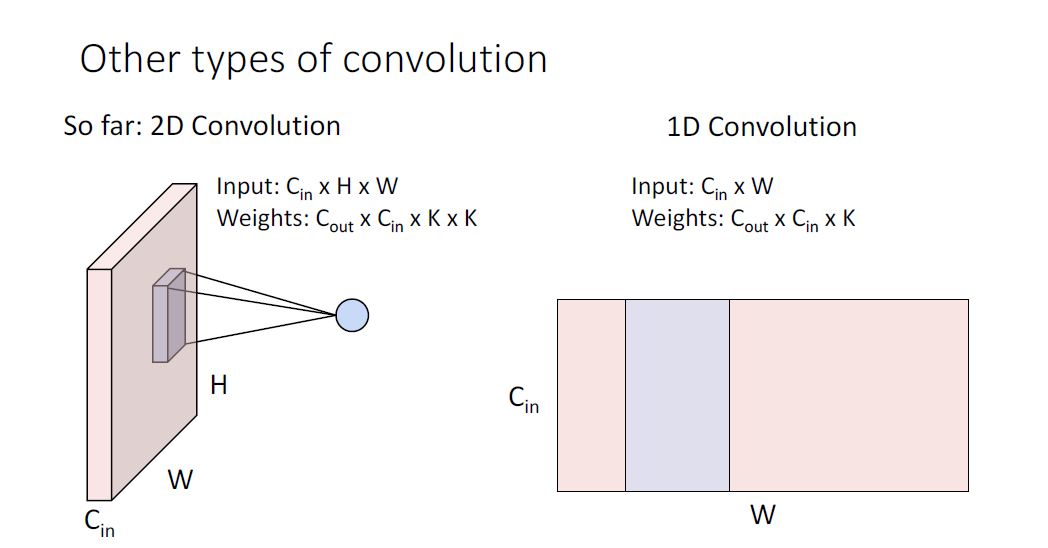
그러나 1D Convolution이라는 것도 있다. input은 2차원으로, 1차원의 채널차원과 1차원의 spatial차원을 가지고 있다.
여기서 필터의 shape은 3차원으로 2D Convlution에서와 마찬가지로 $C_{out}$과 $C_{in}$ 그리고 spatial size인 K를받아 $C_{out} \times C_{in} \times K$가 된다.
1D Convolution은 어떤 텍스트 데이터와 같은 시퀀스형태의 구조를 가진 데이터나 오디오 데이터를 다룰 때 유용하게 사용된다.

또 다른 Convolution으로는 3D Convolution이 있다. 마찬가지로 4차원의 텐서를 입력으로 받고, 필터는 5차원의 구조를 띄게 된다. 3D Convolution는 Point Cloud와 같은 3차원 데이터를 다룰 때 사용한다.

파이토치를 예로 살펴보면, Convolution layer에서는 설정해야 할 하이퍼 파라미터가 다수 존재하게 된다.

또한 1D Conv와 3D Conv도 찾아볼 수 있다.

다음으로 살펴볼 CNN의 요소는 Pooling Layer인데, CNN의 핵심 요소중 하나이다.

Pooling Layer는 학습가능한 가중치가 없는 down sampling layer이다.
spatial size를 줄이는 방법은 앞선대로 Stride를 1보다 크게 해서 Convolution layer를 사용하는 방법도 있지만
Pooling layer를 사용하면 가중치의 사용 없이 spatial size를 줄일 수 있다.
Pooling layer는 Convolution Layer와 비슷한 방식으로 작동하는 하나의 함수로, 각 커널 혹은 필터의 사이즈에 관한 하이퍼 파라미터를 필요로 하고, input tensor에 대해 동일하게 slide over하면서, local receptive filed를 하나의 값으로 뭉개서 downsample을 수행하게 되는 연산이다.

Pooling에는 Average Pooling과 Max Pooling등이 있는데, 대표적인 것은 stride2의 kernel size 2x2인 Max Pooling이다.
stride와 kernel size는 convolution layer와 정확히 동일한 역할을 수행한다.
max pooling이 tensor의 spatial size를 줄이는 방법으로 convolution에 stride를 주는 것 보다 선호되는 이유는
첫번째로 학습해야하는 파라미터가 없다는 점과, 두번째로는 translation-invaraint한 특성때문인데,
Max라는 연산은 단순히 국소 지역에서의 값들중 가장 큰 값을 선택하여 넘기는 것이기 때문에 input image의 사소한 변화에도 동일한 연산 결과를 갖게 되기 때문이다. 따라서 어떠한 문제를 풀고자 하느냐에 따라 이러한 translation-invariant의 성질을 중요하게 작용한다.

Pooling Layer에 대한 요약이다

지금까지 배운 부분만으로 Classic ConvNet을 만들 수 있다.

가장 대표적인 예시가 1998년, 글자체를 인식하기 위해 얀르쿤이 제안 했던 LeNet-5이다.
Input으로는 1x28x28의 이미지가 들어가게 되고(gray-scale의 이미지여서 3채널이 아닌 1채널이다.)
첫번째 요소는 20개의 필터가 사용된 Convolutional Layer이고 SamePadding이 사용되었으며 activation function으로 ReLU가 사용 되었다. 이후 MaxPooling으로 spatial size를 절반으로 줄였다.

이후 Conv-ReLU-MaxPooL이 한번 더 쓰였으며 벡터를 Flatten 시킨 뒤, 이를 Linear Layer-ReLU-Linear Layer에 통과시켜주었다. 전체적인 구조를 살펴보면 레이어를 통과하면서 spatial size는 줄어들지만, 채널 수는 증가해서 데이터의 전체적인 크기 자체는 유지되는 것을 볼 수 있는데, 이것은 Convolutional Layer의 일반적인 특징이다.

이러한 Classic ConvNet의 문제는 훈련 시키기가 어렵다는 것인데, 앞선 예시처럼 Conv-ReLU-MaxPool , Conv-ReLU-MaxPool, Conv-ReLU-MaxPool ... 과 같은 구조가 계속 반복되어 네트워크 "Deep"해지면 수렴하기가 매우 어렵다.
이를 해결하기 위해서 우리는 네트워크에 Nomalization layer를 추가하여 훈련을 더 용이하도록 하게 한다.

Normalization layer의 이름은 Batch Normalization으로 아이디어 자체는 이전 레이어의 output을 zero mean과 unit variance distribution을 가지도록 변환 시킨다.
Batch Normalization의 원 논문(2015)에서는 이 작업이 네트워크의 internal covariate shift를 감소하도록 돕기 위해서 수행하는 것이라고 설명하는데 모델이 학습될 때, 각 레이어에서의 weight가 업데이트되고 다음 feed forward에서는 update된 weight로 출력을 뱉기 때문에 매번 분포가 바뀌게 되는데, 이러한 분포의 변화는 네트워크가 optimization을 어렵게 만든다. 따라서 모든 레이어가 안정된 분포를 가지도록 standardization하는 것이다.
원 논문 이후에는 internal covariate shift의 감소효과가 직접적인 이유가 아닌 Loss surface smoothing효과라고 설명되기도 하는데, 사실은 직까지도 학습이 잘 되게 하는 명확한 이유가 기술되지 않았다.

Batch Normalization을 좀 더 구체적으로 이해 하기 위해서 Fully connected layer의 예시를 들어보면,
Input이 $N$의 Batch를 갖고 각 벡터는 D 차원이라고 가정하면,
서로 다른 각각의 샘플로 구성된 배치에서 각 벡터 요소(slot)들, 데이터들의 평균(empricial mean)을 구한다.
이러한 평균은 벡터와 동일하게 D 차원을 갖는다.
표준편차(standard deviation) 또한 마찬가지로, 우리가 이미 알고 있는 편차의 제곱으로 부터 구한 평균값을 사용하고
이 둘을 이용하여 데이터를 Normalizing하게 된다. 이 때 분모로 나눠주는 값에는 $\epsilon$을 더하여 0으로 나누어지는 것을 방지해준다. (하이퍼 파라미터이긴 하지만, 큰 관심을 두지는 않는다.)

매우 nice한 normalization방법인 것 같지만, layer들의 입장에서는 항상 zero mean과 unit variance를 갖으라는 매우 엄격한 형태의 제한을 두는 것이나 다름이 없다.

이 때문에 Learnable parameter로서, scale parmeter인 $\gamma$와 shifting parameter인 $\beta$를 두게 된다.
만약 $\gamma$가 $\sigma$로 학습되고, $\beta$가 $\mu$로 학습된다면, layer입장에서는 원래의 함수(identity function in expectation)로 되돌아가는것과 동일해서, 네트워크가 필요시 원래의 layer로 되돌아가는 능력을 갖게 되는 셈이다.

그러나 BatchNormalization에는 한가지 문제가 있는데, 다른 연산들과는 다르게 BatchNormalization의 연산은 Batch Size에 의존적인 연산이라는 점이고, 이는 훈련과 추론시에 연산이 각각 다르게 적용된다는 것을 의미한다.

이를 해결하기 위해서 훈련때 지수이동 평균, 지수이동 분산을 저장해서 추론때 이를 사용하게 된다. 이들은 단순한 상수 값으로 배치에 의존적이지 않다.

BatchNormalization의 연산을 자세히 살펴보면 그저 $\sigma$에 의해 scaling되고, $\mu$에 의해서 shifting되는데 이는 단순히 선형 연산과 동일한 기능을 한다는 것을 알 수 있다.
지금까지 두개의 선형 연산은 하나의 선형 연산과 동일한 표현효과를 갖는 것을 배웠다.
따라서 BatchNormalization층은 이전 Linear Layer또는 Convolution layer와 결합하여 하나의 Linear Operator로 작동할 수 있게 되고 BatchNormaliation은 다른 어떤 layer보다 computational cost가 매우 적게 된다.

지금까지 BatchNormalization은 Linear Layer의 예를 들어 설명했지만 Convolutionlaye에 결합되는 BatchNormalization도 있다. 이는 BatchNorm2D 혹은 Spatial Batchnorm이라고도 불리며, 원래의 BatchNorm이 각 배치별 채널의 차원 D의 요소들에 걸쳐 slot을 채웠다면, BatchNorm2D는 각 배치별, 그리고 채널별 slot을 채우게 된다. (HxW가 피쳐로 동작한다.)

BN은 앞선대로 FC layer 혹은 ConvLayer와 같이 결합되어, nonlinearlity를 지닌 활성화 함수 이전에 사용된다.

BatchNorm을 사용함으로써 얻는 이점에 대해서 살펴본다.
BarchNormalization 원논문으로부터 가져온 plot인데, 단순히 BatchNormalization을 추가한 것만으로 학습이 매우 잘되는 것을 알 수 있다.
또한 높은 learning rate를 설정할 수 있으며, 12배에 가까운 빠른 수렴속도를 보인다고 한다.
또한 Normalization의 특성상 초기 initialization에 대해서 강건한 성능을 보이며
Regularization 테크닉의 하나로써 작용한다.
또한 test time에서 FC layer 또는 Convlayer와 결합되어 연산됨으로 오버헤드가 전혀 없다고 한다.

BN에서 명쾌하지 않은 몇가지 지점을 살펴보면, 초기에는 internal covariate shift를 개선하여 optimization을 도왔을 것이라는 제시가 되었지만, 이는 명쾌한 근거는 아니며 아직까지도 어떻게 optimization을 돕는지에 대해서는 명쾌하게 설명된 바가 없다.
또한 train time과 test time에서 다르게 작동하기 때문에 mode설정을 다르게 해야된다던가, 디버깅시 문제가 자주 발생되는 원인 중 하나가 되기도 한다고 한다.
그리고 trainset과 testset에 상당한 imbalance가 존재하는 경우, 잘 작동하지 않을 수 있다고 한다.

BatchNorm의 단점중 하나는 Batch에 의존적인 부분이었는데, 이를 해결한것이 Layer Normalization이다.
LayerNorm은 feature dimension인 D에 따르는 요소들을 Normalize해주는 것으로, 전체 배치에 걸쳐 slot을 채우게 된다.
RNN과 Transformer계열 처럼, Batch가 일정하지 않은 시퀀스 데이터를 다루는 경우 LayerNorm이 사용될 수 있다고 한다.
또한 배치에 의존적이지 않음으로 train time과 test time에 동일하게 작동하는 연산이다.

image를 처리할때 LayerNormalization에 대응되는 Normalization 방법은 Instance Normalization이다.
단순히 spatial dimension인 HxW에 대해서 normalize를 진행한다. 이 역시 배치에 의존적이지 않기 때문에
train time과 test time에서 동일하게 작동한다.

Normalization의 종류들에 대해 훌륭한 직관을 제공하는 그림이다.
BatchNormalization은 각 채널별로 normalize를 하게 되고 (채널별로 다른 값)
LayerNormalizatoin은 각 피쳐별로 normalize를 하게 되고 (배치별로 다른 값)
InstanceNormalization은 각 채널별, 피쳐별로 normalize를 진행한다. (각 채널별, 배치별로 다른 값을 갖게 된다.)

그리고 한가지 더, GroupNormalization이 제안되었는데, 이는 Channel Dimension을 몇가지 그룹으로 묶고, 서로 다른 채널 그룹별로 normalize를 진행하게 된다고 한다.
obejct detection과 같은 task에서 매우 잘 작동한다고 한다.

지금까지 Convolution Network를 이루는 서로 다른 구성요소에 대해서 살펴보았다. 이것들로 CNN Network를 어떻게 만드는 것이 좋을까?

이러한 요소들을 어떻게 결합하는가에 대해서는 다음강에서 다루도록 한다.

'기초 노트 > EECS 498-007 (ComputerVision)' 카테고리의 다른 글
| EECS 498-007 Lecture10: Training Neural Networks Part1 정리 (0) | 2024.04.04 |
|---|---|
| EECS 498-007 Lecture 8: CNN Architectures 정리 (0) | 2024.04.02 |
| EECS 498-007 Lecture 06 : Backpropagation 정리 (0) | 2024.03.21 |
| EECS 498-007 Lecture 05 : Neural Networks 정리 (0) | 2024.03.17 |
| EECS 498-007 Lecture 04 : Optimization 정리 (0) | 2024.03.15 |




